题目内容
已知直线ax﹣by﹣2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则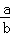 为( )
为( )
| A.3 | B.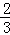 | C.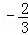 | D.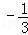 |
D
解析试题分析:由导数的几何意义可求曲线y=x3在(1,1)处的切线斜率k,然后根据直线垂直的条件可求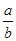 的值. 解:设曲线y=x3在点P(1,1)处的切线斜率为k,则k=f′(1)=3
的值. 解:设曲线y=x3在点P(1,1)处的切线斜率为k,则k=f′(1)=3
因为直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,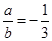 ,故选D.
,故选D.
考点:导数的几何意义
点评:本题主要考查了导数的几何意义:曲线在点(x0,y0)处的切线斜率即为该点处的导数值,两直线垂直的条件的运用.属于基础试题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
设函数f(x)在 处可导,则
处可导,则 等于( )
等于( )
A. | B. | C.- | D.- |
已知曲线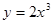 上一点
上一点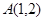 ,则点
,则点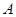 处的切线斜率等于
处的切线斜率等于
A. | B.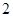 | C.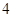 | D.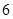 |
过点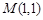 且与曲线
且与曲线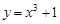 相切的直线方程是( )
相切的直线方程是( )
A.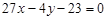 |
B.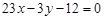 或 或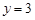 |
C.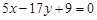 |
D.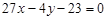 或 或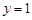 |
已知函数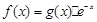 在
在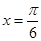 处有极值,则函数
处有极值,则函数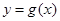 的图象可能是( )
的图象可能是( )
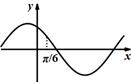
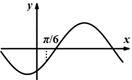

| A. | B. | C. | D. |
已知二次函数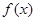 =
=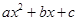 的导数为
的导数为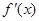 ,
, >0,对任意实数
>0,对任意实数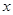 都有
都有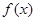 ≥0,则
≥0,则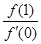 的最小值为( )
的最小值为( )
| A.4 | B.3 | C.8 | D.2 |
曲线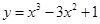 在点
在点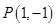 处的切线方程是
处的切线方程是
A.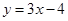 | B.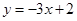 | C.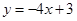 | D.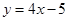 |
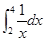 等于( )
等于( )
| A.-2ln 2 | B.2ln 2 | C.-ln 2 | D.ln 2 |
若函数 满足
满足 ,设
,设 ,
, ,则
,则 与
与 的大小关系为
的大小关系为
A. | B. | C. | D. |