题目内容
若函数 满足
满足 ,设
,设 ,
, ,则
,则 与
与 的大小关系为
的大小关系为
A. | B. | C. | D. |
D
解析试题分析:设函数g(x)=xf(x),∵ ,∴
,∴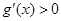 ,即函数g(x)在定义域上单调递增,∵2>1,∴g(2)>g(1),∴2f(2)>f(1) ,∴
,即函数g(x)在定义域上单调递增,∵2>1,∴g(2)>g(1),∴2f(2)>f(1) ,∴ >
> ,故选D
,故选D
考点:本题考查了导数的运用
点评:对于抽象函数的大小比较问题,常常构造函数,然后利用函数的单调性处理

练习册系列答案
相关题目
已知直线ax﹣by﹣2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则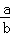 为( )
为( )
| A.3 | B.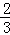 | C.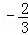 | D.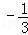 |
设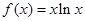 ,若
,若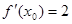 ,则
,则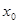 等于( )
等于( )
| A.e2 | B.e | C.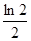 | D.ln2 |
 等于
等于
| A.1 | B.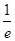 | C. | D. |
若 ,则
,则 等于
等于
A. | B. | C. | D. |
(理科) 如果 的展开式中的常数项为
的展开式中的常数项为 ,则直线
,则直线 与曲线
与曲线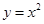 围成图形的面积为( )
围成图形的面积为( )
A. | B.9 | C. | D. |
设函数 ,则该函数曲线在
,则该函数曲线在 处的切线与曲线
处的切线与曲线 围成的封闭图形的面积是 ( )
围成的封闭图形的面积是 ( )
A. | B. | C. | D. |
已知函数 在(1,4)上是减函数,则实数
在(1,4)上是减函数,则实数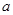 的取值范围是( )
的取值范围是( )
A. | B.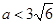 | C. | D. |
已知函数 ,则
,则 ( )
( )
| A.-1 | B.-3 | C.2 | D.-2 |