题目内容
已知二次函数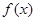 =
=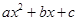 的导数为
的导数为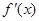 ,
, >0,对任意实数
>0,对任意实数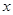 都有
都有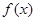 ≥0,则
≥0,则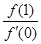 的最小值为( )
的最小值为( )
| A.4 | B.3 | C.8 | D.2 |
D
解析试题分析:先求导,由f′(0)>0可得b>0,因为对于任意实数x都有f(x)≥0,所以结合二次函数的图象可得a>0且b2-4ac≤0,又因为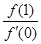 =
=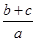 +1,利用均值不等式即可求解解:∵f'(x)=2ax+b,∴f'(0)=b>0;∵对于任意实数x都有f(x)≥0,∴a>0且b2-4ac≤0,∴b2≤4ac,∴c>0;所以
+1,利用均值不等式即可求解解:∵f'(x)=2ax+b,∴f'(0)=b>0;∵对于任意实数x都有f(x)≥0,∴a>0且b2-4ac≤0,∴b2≤4ac,∴c>0;所以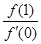 =
=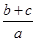 +1
+1 ,此时a=c时取得等号,故选D
,此时a=c时取得等号,故选D
考点:导数的运算,基本不等式
点评:本题考查了求导公式,二次函数恒成立问题以及均值不等式,综合性较强.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
设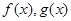 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当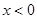 时,
时, ,且
,且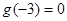 ,则
,则 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
设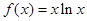 ,若
,若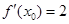 ,则
,则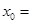 ( )
( )
A.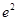 | B.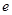 | C.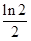 | D.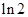 |
设曲线 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为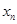 ,则
,则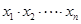 的值为( )
的值为( )
A.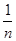 | B.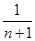 | C.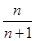 | D.1 |
已知直线ax﹣by﹣2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则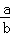 为( )
为( )
| A.3 | B.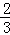 | C.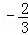 | D.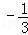 |
若 ,则
,则 等于
等于
| A.2 | B.-2 | C. | D. |
已知曲线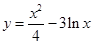 的一条切线的斜率为
的一条切线的斜率为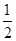 ,则切点的横坐标为( )
,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D.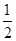 |
已知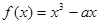 在(-∞,-1)上单调递增,则
在(-∞,-1)上单调递增,则 的取值范围是( )
的取值范围是( )
A. <3 <3 | B.  3 3 | C. >3 >3 | D. 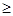 3 3 |
(理科) 如果 的展开式中的常数项为
的展开式中的常数项为 ,则直线
,则直线 与曲线
与曲线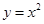 围成图形的面积为( )
围成图形的面积为( )
A. | B.9 | C. | D. |