题目内容
已知函数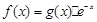 在
在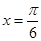 处有极值,则函数
处有极值,则函数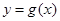 的图象可能是( )
的图象可能是( )
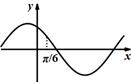
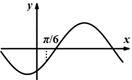

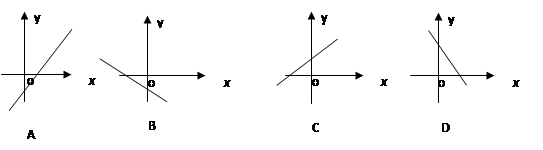
| A. | B. | C. | D. |
A
解析试题分析:因为,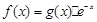 ,令
,令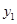 =
=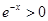 是减函数,
是减函数,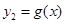 。
。
图象B中,在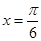 处,
处,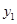 和
和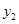 绝对值为正且都处于减小过程中,两都相乘后的函数f(x)为正且是处于减小过程,不可能存在极值;
绝对值为正且都处于减小过程中,两都相乘后的函数f(x)为正且是处于减小过程,不可能存在极值;
图象C中,在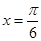 处,
处,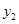 为负且绝对值持续减小,而
为负且绝对值持续减小,而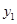 也是持续减小,相乘后f(x)绝对值仍为负且继续减小,不存在极值;
也是持续减小,相乘后f(x)绝对值仍为负且继续减小,不存在极值;
图象D中,在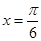 处,
处,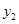 由负变正而
由负变正而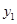 持续减小,f(x)将由负变正,虽不能肯定之后函数走势,但该处不可能是极值点;
持续减小,f(x)将由负变正,虽不能肯定之后函数走势,但该处不可能是极值点;
图象A所示情形,在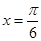 处,
处,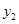 为负但绝对值继续增加,而
为负但绝对值继续增加,而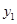 是持续减小,两者相乘后f(x)保持为负但绝对值可能不会再增大,有可能存在极值。
是持续减小,两者相乘后f(x)保持为负但绝对值可能不会再增大,有可能存在极值。
考点:本题主要考查函数极值存在的条件,函数的图象。
点评:中档题,结合函数图象,定性估计函数极值的情况,具有“猜测”成分。

练习册系列答案
相关题目
函数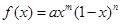 在区间
在区间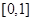 上的图像如图所示,则
上的图像如图所示,则 、
、 的值可能是( )
的值可能是( )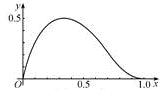
A.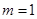 , , |
B.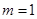 , ,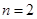 |
C. , , |
D. , , |
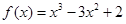 在区间
在区间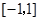 上的最大值是( )
上的最大值是( )
A.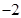 | B.0 | C.2 | D.4 |
若函数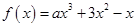 恰有三个单调区间,则实数
恰有三个单调区间,则实数 的取值范围为 ( )
的取值范围为 ( )
A.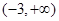 | B.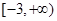 | C.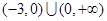 | D.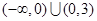 |
在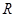 上可导的函数
上可导的函数 的图形如图所示,则关于
的图形如图所示,则关于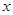 的不等式
的不等式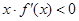 的解集为( )
的解集为( )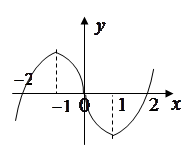
A.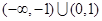 | B.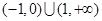 |
C.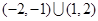 | D.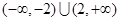 |
已知直线ax﹣by﹣2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则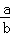 为( )
为( )
| A.3 | B.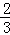 | C.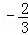 | D.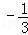 |
已知函数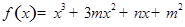 在
在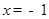 时有极值为0,则m+n=( )
时有极值为0,则m+n=( )
| A.11 | B.4或11 | C.4 | D.8 |
若 ,则
,则 等于
等于
A. | B. | C. | D. |