Question

16．若x满足$\sqrt{2}$cos（$\frac{3π}{4}$-x）=m，-π≤x≤π，为使满足条件的x的值：
（1）存在；
（2）有且只有一个；
（3）有两个不同的值；
（4）有三个不同的值．
分别求实数m的取值范围．

Answer 1

分析 由题意可得cos（x+$\frac{π}{4}$）=-$\frac{\sqrt{2}}{2}$m∈[-1，1]，再结合余弦函数的图象的特征，求出各种情况下m的取值范围．

解答 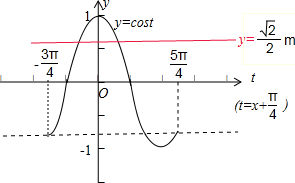解：∵$\sqrt{2}$cos（$\frac{3π}{4}$-x）=m，即 cos（x-$\frac{3π}{4}$）=$\frac{\sqrt{2}}{2}m$，即 cos（x+$\frac{π}{4}$）=-$\frac{\sqrt{2}}{2}$m．
根据-π≤x≤π，可得x+$\frac{π}{4}$∈[-$\frac{3π}{4}$，$\frac{5π}{4}$]，故cos（x+$\frac{π}{4}$）=-$\frac{\sqrt{2}}{2}$m∈[-1，1]．
（1）若使满足条件的x的值存在，则m∈[-$\sqrt{2}$，$\sqrt{2}$]．
（2）若使满足条件的x的值有且只有一个，则-$\frac{\sqrt{2}}{2}$m=±1，求得m=±$\sqrt{2}$．
（3）若使满足条件的x的值有2个，则-$\frac{\sqrt{2}}{2}$m∈（-$\frac{\sqrt{2}}{2}$，1），求得m∈（-$\sqrt{2}$，1）．
（4）若使满足条件的x的值有3个，则-$\frac{\sqrt{2}}{2}$m=-$\frac{\sqrt{2}}{2}$，求得m=1．

点评 本题主要考查余弦函数的图象，体现了转化、数形结合的数学思想，属于中档题．