��Ŀ����
��2008•������һģ����֪������D�Ķ�������Բ
+
=1�����ģ����������Բ���ҽ����غϣ�
��1����������D�ķ��̣�
��2����֪��ֱ��l����P��4��0������������D��A��B���㣬����ԭ��OΪPQ�е㣬��֤����AQP=��BQP��
��3���Ƿ���ڴ�ֱ��x���ֱ��m����APΪֱ����Բ���صõ��ҳ���Ϊ��ֵ��������ڣ����m�ķ��̣���������ڣ�˵�����ɣ�
| x2 |
| 4 |
| y2 |
| 3 |
��1����������D�ķ��̣�
��2����֪��ֱ��l����P��4��0������������D��A��B���㣬����ԭ��OΪPQ�е㣬��֤����AQP=��BQP��
��3���Ƿ���ڴ�ֱ��x���ֱ��m����APΪֱ����Բ���صõ��ҳ���Ϊ��ֵ��������ڣ����m�ķ��̣���������ڣ�˵�����ɣ�
��������1�������⣬�������߷���Ϊy2=2px��p��0������a2-b2=4-3=1����c=1���ɴ������������D�ķ��̣�
��2����A��x1��y1����B��x2��y2��������OΪPQ֮�е㣬�ʵ�l��x��ʱ�������ߵĶԳ���֪��AQP=��BQP����l����ֱx��ʱ����l��y=k��x-4������
����k2x2-4��2k2+1��x+16k2=0���ɴ��ܹ�֤����AQP=��BQp��
��3�������ֱ��m+x=a�������⣬��Բ��M(
��
)����M��ֱ��x=a�Ĵ��ߣ�����ΪE����|EG|2=|MG|2-|ME|2���ɴ��ܹ���������ֱ��m��x=3�������⣮
��2����A��x1��y1����B��x2��y2��������OΪPQ֮�е㣬�ʵ�l��x��ʱ�������ߵĶԳ���֪��AQP=��BQP����l����ֱx��ʱ����l��y=k��x-4������
|
��3�������ֱ��m+x=a�������⣬��Բ��M(
| x1+4 |
| 2 |
| y1 |
| 2 |
�������С������14�֣�
��1���⣺�����⣬���������߷���Ϊy2=2px��p��0����
��a2-b2=4-3=1����c=1��
�������ߵĽ���Ϊ��1��0������p=2��
��������D�ķ���Ϊy2=4x������4�֣�
��2��֤������A��x1��y1����B��x2��y2����
����OΪPQ֮�е㣬�ʵ�l��x��ʱ���������ߵĶԳ���֪��һ���С�AQP=��BQP��
��l����ֱx��ʱ����l��y=k��x-4����
��
����k2x2-4��2k2+1��x+16k2=0��
��
��
��kAQ=
=
��
kBQ=
=
��
��kAQ+kBQ=
=
=0��
���AQP=��BQP��
����֤֪����AQP=��BQP
��3���⣺�����ֱ��m+x=a�������⣬
��Բ��M(
��
)��
��M��ֱ��x=a�Ĵ��ߣ�����ΪE��
��|EG|2=|MG|2-|ME|2��
��|EG|2=|MA|2-|ME|2
=
-(
-a)2
=
y12+
+a(x1+4)-a2
=x1-4x1+a(x1+4)-a2
=(a-3)x1+4a-a2��
��a=3ʱ��|EG|2=3��
��ʱֱ��m����APΪֱ����Բ�صõ��ҳ���Ϊ��ֵ2
������13�֣�
��˴���ֱ��m��x=3�������⡭��14�֣�
��1���⣺�����⣬���������߷���Ϊy2=2px��p��0����
��a2-b2=4-3=1����c=1��
�������ߵĽ���Ϊ��1��0������p=2��
��������D�ķ���Ϊy2=4x������4�֣�
��2��֤������A��x1��y1����B��x2��y2����
����OΪPQ֮�е㣬�ʵ�l��x��ʱ���������ߵĶԳ���֪��һ���С�AQP=��BQP��
��l����ֱx��ʱ����l��y=k��x-4����
��
|
��
|
��kAQ=
| y1 |
| x1+4 |
| k(x1-4) |
| x1+4 |
kBQ=
| y2 |
| x2+4 |
| k(x2-4) |
| x2+4 |
��kAQ+kBQ=
| k(2x1x2-32) |
| (x1+4)(x2+4) |
| k(2•16-32) |
| (x1+4)(x2+4) |
���AQP=��BQP��
����֤֪����AQP=��BQP
��3���⣺�����ֱ��m+x=a�������⣬
��Բ��M(
| x1+4 |
| 2 |
| y1 |
| 2 |
��M��ֱ��x=a�Ĵ��ߣ�����ΪE��
��|EG|2=|MG|2-|ME|2��
��|EG|2=|MA|2-|ME|2
=
| (x1-4)2+y12 |
| 4 |
| x1+4 |
| 2 |
=
| 1 |
| 4 |
| (x1-4)2-(x1+4)2 |
| 4 |
=x1-4x1+a(x1+4)-a2
=(a-3)x1+4a-a2��
��a=3ʱ��|EG|2=3��
��ʱֱ��m����APΪֱ����Բ�صõ��ҳ���Ϊ��ֵ2
| 3 |
��˴���ֱ��m��x=3�������⡭��14�֣�
���������⿼�������߷��̵���ֱ�ߺ������ߵ�λ�ù�ϵ�������������������������֤���������黯����ת��˼�룮����ѧ˼ά��Ҫ��Ƚϸߣ���һ����̽���ԣ��ۺ���ǿ���Ѷȴ��Ǹ߿����ص㣮����ʱҪ�������⣬��ϸ���

��ϰ��ϵ�д�
�����Ŀ
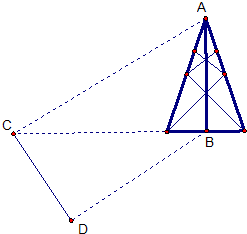 ��2008•������һģ����ͼ�������Ӷ�������ABʱ������ѡ������B��ͬһˮƽ���ڵ��������C��D���ֲ�á�BCD=75�㣬��BDC=60�㣬CD=s�����ڵ�C�������A������Ϊ30�㣬������AB��
��2008•������һģ����ͼ�������Ӷ�������ABʱ������ѡ������B��ͬһˮƽ���ڵ��������C��D���ֲ�á�BCD=75�㣬��BDC=60�㣬CD=s�����ڵ�C�������A������Ϊ30�㣬������AB�� ��2008•������һģ�����һ�������������ͼ����ͼ��ʾ����λ���ȣ�cm��˼�����ı�����ǣ�������
��2008•������һģ�����һ�������������ͼ����ͼ��ʾ����λ���ȣ�cm��˼�����ı�����ǣ�������