题目内容
14.已知△ABC的内角A,B,C的对边分别为a,b,c,且满足$cosA=\frac{3}{5}$,$\overrightarrow{AB}•\overrightarrow{AC}=3$.则△ABC的面积2.分析 由已知可得$|\overrightarrow{AB}||\overrightarrow{AC}|=5$,利用平方关系求出sinA,代入三角形面积公式得答案.
解答 解:在△ABC中,由cosA=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}=\frac{3}{|\overrightarrow{AB}||\overrightarrow{AC}|}=\frac{3}{5}$,
得$|\overrightarrow{AB}||\overrightarrow{AC}|=5$,
且sinA=$\sqrt{1-co{s}^{2}A}=\sqrt{1-(\frac{3}{5})^{2}}=\frac{4}{5}$,
∴${S}_{△ABC}=\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|sinA$=$\frac{1}{2}×5×\frac{4}{5}=2$.
故答案为:2.
点评 本题考查平面向量的数量积运算,考查了三角形面积的求法,是中档题.

练习册系列答案
相关题目
2.下列方程中表示相同曲线的是( )
| A. | y=x,$\frac{y}{x}=1$ | B. | y=2x,$y=2\sqrt{x^2}$ | C. | |y|=|x|,$\sqrt{y}=\sqrt{x}$ | D. | |y|=|x|,y2=x2 |
19.点P(1,2,3)到原点的距离是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2 |
6.已知幂函数y=f(x)的图象过点$(2,\sqrt{2})$,则f(9)=( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 9 | D. | $\frac{1}{9}$ |
3.已知f(x)=x2+ax在[0,1]上是单调递减函数,则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-∞,-2] | C. | [0,+∞) | D. | [2,+∞) |
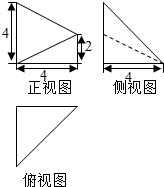 已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A-BCED的体积为16.将直角三角形△ABD绕斜边AD旋转一周,则BD=2;该旋转体的表面积为$\frac{32+8\sqrt{2}}{3}π$.
已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A-BCED的体积为16.将直角三角形△ABD绕斜边AD旋转一周,则BD=2;该旋转体的表面积为$\frac{32+8\sqrt{2}}{3}π$.