题目内容
如图所示,已知A(-1,0),B(1,0),直线l垂直AB于A点,P为l上一动点,点N为线段BP上一点,且满足![]() =λ
=λ![]() (λ>0),
(λ>0),![]() ·
·![]() =0.
=0.

(1)求动点M的轨迹方程C;
(2)在上述曲线内是否存在一点Q,若过点Q的直线与曲线C交于两点E、F,使得以EF为直径的圆都与l相切?若存在,求出点Q的坐标;若不存在,请说明理由.
解:由![]() =2
=2![]() 知点N为BP中点,
知点N为BP中点,
由![]() =λ
=λ![]() (λ>0),知
(λ>0),知![]() ∥
∥![]() 且点M与B位于l同侧.
且点M与B位于l同侧.
因为![]() ·
·![]() =0,所以
=0,所以![]() ⊥
⊥![]() .
.
由此知MN为线段BP的垂直平分线,所以应有|MB|=|MP|.
由抛物线定义知点M的轨迹为抛物线,点B为焦点,直线l为准线,
(1)因为A(-1,0),B(1,0),所以l:x=-1.
抛物线方程为y2=4x,即为点M的轨迹方程.
(2)存在点Q,即为焦点B(1,0).
证明如下:设EF为抛物线的焦点弦,设其中点为H,分别由E、H、F向l作垂线,垂足分别为R、S、T.

由梯形的中位线知:
|HS|=![]() (|ER|+|FT|)=
(|ER|+|FT|)=![]() (|EB|+|FB|)=
(|EB|+|FB|)=![]() |EF|,
|EF|,
即以EF为直径的圆的圆心到直线l的距离等于半径.
所以以EF为直径的圆必与直线l相切.
所以存在点Q,其坐标为(1,0).

练习册系列答案
相关题目
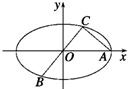 如图所示,已知A,B,C是椭圆
如图所示,已知A,B,C是椭圆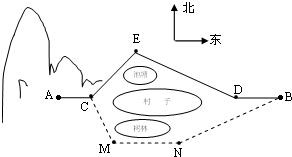 某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.
某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°. 水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为
水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为 如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且 如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E
如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E