题目内容
 水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为
水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为| 5 |
| 2 |
| 5 |
| 2 |
分析:由已知中直观图中线段的长,可分析出△ABC实际为一个直角边长分别为3,4的直角三角形,进而根据勾股定理求出斜边,结合直角三角形斜边上的中线等于斜边的一半可得答案.
解答:解:∵直观图中A′C′=3,B′C′=2,
∴Rt△ABC中,AC=3,BC=4
由勾股定理可得AB=5
则AB边上的中线的实际长度为
故答案为:
∴Rt△ABC中,AC=3,BC=4
由勾股定理可得AB=5
则AB边上的中线的实际长度为
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查的知识点是斜二测画法直观图,其中掌握斜二测画法直观图与原图中的线段关系是解答的关键.

练习册系列答案
相关题目
 如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=
如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=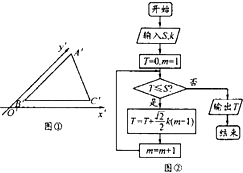 如图①,利用斜二侧画法得到水平放置的△ABC的直观图△A′B′C′,其中A′B′∥y′轴,B′C′∥x′轴.若A′B′=B′C′=3,设△ABC的面积为S,△A′B′C的面积为S′,记S=kS′,执行如图②的框图,则输出T的值( )
如图①,利用斜二侧画法得到水平放置的△ABC的直观图△A′B′C′,其中A′B′∥y′轴,B′C′∥x′轴.若A′B′=B′C′=3,设△ABC的面积为S,△A′B′C的面积为S′,记S=kS′,执行如图②的框图,则输出T的值( )