题目内容
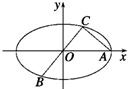
 如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且| AC |
| BC |
(I)建立适当的坐标系,求椭圆方程;
(II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明:存在实数λ,使
| PQ |
| AB |
分析:(Ⅰ)设椭圆的标准方程,根据长轴求得a,点A是长轴的一个顶点可求得A的坐标.根据
•
=0 , |
|=2|
|判断△AOC是等腰直角三角形,进而求得C的坐标代入椭圆的方程求得b,最后可得椭圆的方程.
(Ⅱ)设直线PC的方程与椭圆方程联立,消元后根据△>0判断k的范围.设点P(x1,y1)由韦达定理可求得x1和y1关于k的表达式,直线CP、CQ与x轴围成底边在x轴上的等腰三角形推断直线CP、CQ的斜率互为相反数,进而得到k的范围,同样的设点Q(x2,y2),根据韦达定理求得x2和y2关于k的表达式,根据椭圆是中心对称图形求得点B的坐标,根据
和
关系得证.
| AC |
| BC |
| BC |
| AC |
(Ⅱ)设直线PC的方程与椭圆方程联立,消元后根据△>0判断k的范围.设点P(x1,y1)由韦达定理可求得x1和y1关于k的表达式,直线CP、CQ与x轴围成底边在x轴上的等腰三角形推断直线CP、CQ的斜率互为相反数,进而得到k的范围,同样的设点Q(x2,y2),根据韦达定理求得x2和y2关于k的表达式,根据椭圆是中心对称图形求得点B的坐标,根据
| PQ |
| AB |
解答:解:(I)以O为原点,OA为X轴建立直角坐标系,设A(2,0),则椭圆方程为
+
=1…2′
∵O为椭圆中心,∴由对称性知|OC|=|OB|
又∵
•
=0,∴AC⊥BC
又∵|BC|=2|AC|∴|OC|=|AC|
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1)∴点B的坐标为(-1,-1)…4
将C的坐标(1,1)代入椭圆方程得b2=
,
则求得椭圆方程为
+
=1…6′
(II)由于∠PCQ的平分线垂直于OA(即垂直于x轴),不妨设PC的斜率为k,则QC的斜率为-k,因此PC、QC的直线方程分别为y=k(x-1)+1,y=-k(x-1)+1
由
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0*)…8′
∵点C(1,1)在椭圆上,
∴x=1是方程(*)的一个根,∴xP•1=
即xP=
同理xQ=
…9′
∴直线PQ的斜率为
=
=
=
(定值)…11′
又∠ACB的平分线也垂直于OA
∴直线PQ与AB的斜率相等(∵kAB=
)
∴向量
∥
,即总存在实数λ,使
=λ
成立.…12′
| x2 |
| 4 |
| y2 |
| b2 |
∵O为椭圆中心,∴由对称性知|OC|=|OB|
又∵
| AC |
| BC |
又∵|BC|=2|AC|∴|OC|=|AC|
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1)∴点B的坐标为(-1,-1)…4
将C的坐标(1,1)代入椭圆方程得b2=
| 4 |
| 3 |
则求得椭圆方程为
| x2 |
| 4 |
| 3y2 |
| 4 |
(II)由于∠PCQ的平分线垂直于OA(即垂直于x轴),不妨设PC的斜率为k,则QC的斜率为-k,因此PC、QC的直线方程分别为y=k(x-1)+1,y=-k(x-1)+1
由
|
∵点C(1,1)在椭圆上,
∴x=1是方程(*)的一个根,∴xP•1=
| 3k2-6k-1 |
| 3k2+1 |
| 3k2-6k-1 |
| 3k2+1 |
同理xQ=
| 3k2+6k-1 |
| 3k2+1 |
∴直线PQ的斜率为
| yP-yQ |
| xP-xQ |
| k(xP+xQ)-2k |
| xP-xQ |
k•
| ||
|
| 1 |
| 3 |
又∠ACB的平分线也垂直于OA
∴直线PQ与AB的斜率相等(∵kAB=
| 1 |
| 3 |
∴向量
| PQ |
| AB |
| PQ |
| AB |
点评:本题以向量为载体,主要考查了椭圆的标准方程和平面向量的知识.能考查学生综合运用所学知识的能力.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图所示,已知A,B,C是椭圆
如图所示,已知A,B,C是椭圆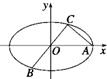 如图所示,已知A、B、C是椭圆E:
如图所示,已知A、B、C是椭圆E: 如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E
如图所示,已知A,B,C是圆O上三个点,AB弧等于BC弧,D为弧AC上一点,过点A做圆O的切线交BD延长线于E