题目内容
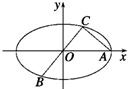如图所示，已知A，B，C是椭圆E：| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
（Ⅰ）求点C的坐标及椭圆E的方程；
（Ⅱ）若椭圆E上存在两点P，Q，使得∠PCQ的平分线总是垂直于x轴，试判断向量
| PQ |
| AB |
分析：（Ⅰ）根据|BC|=2|AC|，且BC经过O可推断出|OC|=|AC|，进而根据A(2
，0)，∠ACB=90°求得C点的坐标，将a及C点坐标代入椭圆方程求得b，则椭圆的方程可得．
（Ⅱ）根据∠PCQ的平分线总垂直于x轴，可知PC与CQ所在直线关于直线x=
对称，设直线PC的斜率为k，则直线CQ的斜率为-k，进而可表示出直线PC的方程和直线CQ的方程分别于椭圆方程联立，根据C点坐标且在椭圆上，可利用韦达定理求得xQ和xp的表达式，进而求得B的坐标，则直线AB的斜率可求得，进而可知kAB=kPQ，推断出向量
与向量
共线．
| 3 |
（Ⅱ）根据∠PCQ的平分线总垂直于x轴，可知PC与CQ所在直线关于直线x=
| 3 |
| PQ |
| AB |
解答：解：（Ⅰ）∵|BC|=2|AC|，且BC经过O（0，0），
∴|OC|=|AC|．又A(2
，0)，∠ACB=90°，
∴C(
，
)，
∵a=2
，将a=2
及C点坐标代入椭圆方程得
+
=1，∴b2=4，
∴椭圆E的方程为：
+
=1．
（Ⅱ）对于椭圆上两点P，Q，
∵∠PCQ的平分线总垂直于x轴，
∴PC与CQ所在直线关于直线x=
对称，设直线PC的斜率为k，则直线CQ的斜率为-k，
∴直线PC的方程为y-
=k(x-
)，
即y=k(x-
)+
．①
直线CQ的方程为y=-k(x-
)+
．②
将①代入
+
=1，
得(1+3k2)x2+6
k(1-k)x+9k2-18k-3=0，③
∵C(
，
)在椭圆上，
∴x=
是方程③的一个根．
∴xP•
=
，
∴xP=
，
同理可得，xQ=
，
∴kPQ=
=
=
．
∵C(
，
)，
∴B(-
，-
)，
又A(2
，0)，
∴kAB=
=
，
∴kAB=kPQ，∴向量
与向量
共线．
∴|OC|=|AC|．又A(2
| 3 |
∴C(
| 3 |
| 3 |
∵a=2
| 3 |
| 3 |
| 3 |
| 12 |
| 3 |
| b2 |
∴椭圆E的方程为：
| x2 |
| 12 |
| y2 |
| 4 |
（Ⅱ）对于椭圆上两点P，Q，
∵∠PCQ的平分线总垂直于x轴，
∴PC与CQ所在直线关于直线x=
| 3 |
∴直线PC的方程为y-
| 3 |
| 3 |
即y=k(x-
| 3 |
| 3 |
直线CQ的方程为y=-k(x-
| 3 |
| 3 |
将①代入
| x2 |
| 12 |
| y2 |
| 4 |
得(1+3k2)x2+6
| 3 |
∵C(
| 3 |
| 3 |
∴x=
| 3 |
∴xP•
| 3 |
| 9k2-18k-3 |
| 1+3k2 |
∴xP=
| 9k2-18k-3 | ||
|
同理可得，xQ=
| 9k2+18k-3 | ||
|
∴kPQ=
| y Q-yP |
| xQ-xP |
-k(xQ+xP)+2
| ||
| xQ-xP |
| 1 |
| 3 |
∵C(
| 3 |
| 3 |
∴B(-
| 3 |
| 3 |
又A(2
| 3 |
∴kAB=
| ||
3
|
| 1 |
| 3 |
∴kAB=kPQ，∴向量
| PQ |
| AB |
点评：本题主要考查了直线与圆锥曲线的综合问题．考查了学生综合分析问题和基本的运算能力．
练习册系列答案
53随堂测系列答案
相关题目
如图所示，已知A、B、C是椭圆E：
如图所示，已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个端点，BC过椭圆中心O，且
如图所示，已知A，B，C是圆O上三个点，AB弧等于BC弧，D为弧AC上一点，过点A做圆O的切线交BD延长线于E
=1（a＞b＞0)上的三点，其中点 
，0）,BC过椭圆的中心O，且AC⊥BC，|BC|=2|AC|.
与
是否共线，并给出证明. 