题目内容
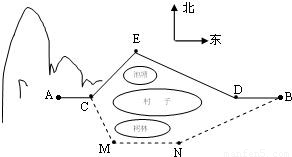
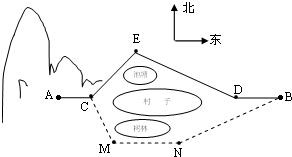 某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.
某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.(I)求CD的长.
(II)在运作了一段时间后,发现在运输车经过公路CE,ED时对池塘有污染..需要另建公路ACMNB.为了不破坏树林,必须要求CM=3km,∠CMN=135°,∠MNB=150°MN∥AC.求建这条新的公路中MN的长.
分析:(I)在△CED中,利用余弦定理根据CE,BD和∠CED求得CD.
(II)过D作DF∥BN交NM与F,MG∥BN,交CD与G,则∠FDC=∠MGC=30°,∠MCG=45°,进而求得∠CMG,进而在△CMG中,由正弦定理求得CG,则GD可求,最后把MF和FN相加即可.
(II)过D作DF∥BN交NM与F,MG∥BN,交CD与G,则∠FDC=∠MGC=30°,∠MCG=45°,进而求得∠CMG,进而在△CMG中,由正弦定理求得CG,则GD可求,最后把MF和FN相加即可.
解答:解:(I)在△CED中,由余弦定理可知
CD2=4+9-2×2×3×(-
)=19
∴CD=
km
(II)过D作DF∥BN交NM与F,MG∥BN,交CD与G,则∠FDC=∠MGC=30°
∠MCG=45°,
∴∠CMG=180°-30°-45°=105°
在△CMG中,由正弦定理可知
=
∴CG=
∴MF=DG=
-
∵FN=BD=2
∴MN=
-
+2km.
CD2=4+9-2×2×3×(-
| 1 |
| 2 |
∴CD=
| 19 |
(II)过D作DF∥BN交NM与F,MG∥BN,交CD与G,则∠FDC=∠MGC=30°
∠MCG=45°,
∴∠CMG=180°-30°-45°=105°
在△CMG中,由正弦定理可知
| CG |
| sin105° |
| CM |
| sin30° |
∴CG=
3
| ||||
| 2 |
∴MF=DG=
| 19 |
3
| ||||
| 2 |
∵FN=BD=2
∴MN=
| 19 |
3
| ||||
| 2 |
点评:本题主要考查了解三角形的实际应用.考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某高速公路旁边B处有一栋楼房,某人在距地面100米的32楼阳台A处,用望远镜路上的车辆,上午11时测得一客车位于楼房北偏东15°方向上,且俯角为30°的C处,10秒后测得该客车位于楼房北偏西75°方向上,且俯角为45°的D处.(假设客车匀速行驶)
某高速公路旁边B处有一栋楼房,某人在距地面100米的32楼阳台A处,用望远镜路上的车辆,上午11时测得一客车位于楼房北偏东15°方向上,且俯角为30°的C处,10秒后测得该客车位于楼房北偏西75°方向上,且俯角为45°的D处.(假设客车匀速行驶)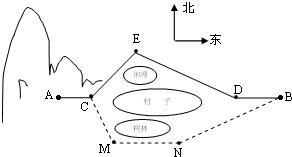 某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.
某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.