题目内容
16.已知($\sqrt{x}$+$\frac{1}{2\sqrt{x}}$)n前三项的系数成等差数列,求n的值以及中间项.分析 由条件根据通项公式求得2${C}_{n}^{1}$•2-1=${C}_{n}^{0}$+${C}_{n}^{2}$•2-2,可得n=8,从而求得它的中间项.
解答 解:根据($\sqrt{x}$+$\frac{1}{2\sqrt{x}}$)n的通项公式为Tr+1=${C}_{n}^{r}$•2-r•${x}^{\frac{n-2r}{2}}$的前三项的系数成等差数列,
可得 2${C}_{n}^{1}$•2-1=${C}_{n}^{0}$+${C}_{n}^{2}$•2-2,求得n=1(舍去)或n=8,
故它的中间项为T5=${C}_{8}^{4}$•2-4=70.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
1.甲、乙、丙三人值周一至周六的班,每人值两天班,若甲不值周一,乙不值周六,则可排出不同的值班表数为( )
| A. | 6 | B. | 12 | C. | 42 | D. | 90 |
19.不等式2kx2+kx-$\frac{3}{8}$<0对任何实数x恒成立,则k的取值范围是( )
| A. | (-3,0] | B. | (-3,0) | C. | [-3,0] | D. | [-3,0) |
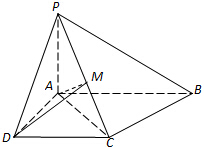 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.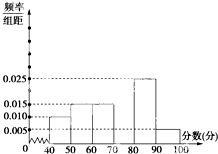 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: