题目内容
11.不等式(x+2)(x-3)>0的解集为(-∞,-2)∪(3,+∞).分析 解得对应方程的根,由三个二次的关系可得.
解答 解:∵方程(x+2)(x-3)=0的两根为-2和3,
∴不等式(x+2)(x-3)>0的解集为:(-∞,-2)∪(3,+∞),
故答案为:(-∞,-2)∪(3,+∞).
点评 本题考查一元二次不等式的解集,属基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.定义域为R的函数f(x)满足f(x+2)=4f(x).x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x}&{x∈[0,1)}\\{lo{g}_{\sqrt{2}}(x+1)}&{x∈[1,2)}\end{array}\right.$,若x∈[-2,0)对任意的t∈[1,2)都有 f(x)≥$\frac{t}{16}-\frac{a}{8{t}^{2}}$成立,则实数a的取值范围是( )
| A. | (-∞,2] | B. | [12,+∞) | C. | (-∞,6] | D. | [6,+∞) |
6.直线x=1,x=2,y=0与曲线y=$\frac{1}{x(x+1)}$围成图形的面积为( )
| A. | ln2 | B. | ln$\frac{4}{3}$ | C. | ln3 | D. | ln3-ln2 |
1.如果函数f(x)=ax+b的图象经过第一、二、四象限,不经过第三象限,那么一定有( )
| A. | 0<a<1,-1<b<0 | B. | 0<a<1,b<-1 | C. | a>1,b<-1 | D. | a>1,-1<b<0 |
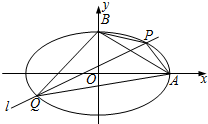 已知平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点和上顶点分别为A,B,椭圆的离心率为$\frac{\sqrt{3}}{2}$,且过点(1,$\frac{\sqrt{3}}{2}$).
已知平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点和上顶点分别为A,B,椭圆的离心率为$\frac{\sqrt{3}}{2}$,且过点(1,$\frac{\sqrt{3}}{2}$).