题目内容
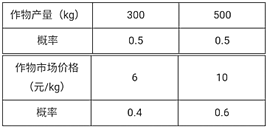
【题目】在一块耕地上种植一种作物，每季种植成本为1000元，此作物的市场价格和这块地上的产量均具有随机性，且互不影响，其具体情况如下表：
（1）设
表示在这块地上种植1季此作物的利润，求的分布列；
（2）若在这块地上连续3季种植此作物，求这3季中至少有2季的利润不少于2000元的概率.
【答案】（1）分布列见解析；（2）
.
【解析】
试题（1）设
表示事件“作物产量为300
”，
表示事件“作物市场价格为6元
”
由题设得4000，2000,800，结合概率公式计算出对应的概率，得出分布列；
（2）设
表示事件“第
季利润不少于2000元”
，由题意知：
相互独立，由（1）知
，3季利润均不少于2000元的概率为:
，3季中有2季利润不少于2000元的概率为：
，根据互斥事件概率的加法公式得：这3季中至少有2季的利润不少于2000元的概率为：
试题解析：（1）设表示事件“作物产量为300”，表示事件“作物市场价格为6元”
由题设知：
，
因为利润=产量
市场价格-成本
所以
所以可能的取值为
，
，
,
,
,
所以的分布列为
| 4000 | 2000 | 800 |
| 0.3 | 0.5 | 0.2 |
（2）设表示事件“第季利润不少于2000元”，
由题意知：相互独立，由（1）知
3季利润均不少于2000元的概率为:
3季中有2季利润不少于2000元的概率为：
所以，这3季中至少有2季的利润不少于2000元的概率为：
口算小状元口算速算天天练系列答案
【题目】政府工作报告指出，2018年我国深入实施创新驱动发展战略，创新能力和效率进一步提升；2019年要提升科技支撑能力，健全以企业为主体的产学研一体化创新机制.某企业为了提升行业核心竞争力，逐渐加大了科技投入；该企业连续6年来的科技投入
（百万元）与收益
（百万元）的数据统计如下：
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 |
|
|
|
|
|
|
根据散点图的特点，甲认为样本点分布在指数曲线
的周围，据此他对数据进行了一些初步处理，如下表：
|
|
|
|
|
|
|
|
|
|
|
|
其中
，
.
(1)（i）请根据表中数据，建立关于
的回归方程（保留一位小数）；
（ii）根据所建立的回归方程，若该企业想在下一年的收益达到2亿，则科技投入的费用至少要多少（其中
）？
(2)乙认为样本点分布在二次曲线
的周围，并计算得回归方程为
，以及该回归模型的相关指数
，试比较甲、乙两位员工所建立的模型，谁的拟合效果更好.
附：对于一组数据
，
，…，
，其回归直线方程
的斜率和截距的最小二乘估计分别为
，
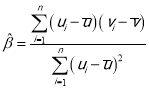，相关指数：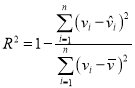
.
【题目】计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量
(年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上.其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.
（1）求未来4年中，至多1年的年入流量超过120的概率；
（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量
限制，并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行，则该台年利润为5000万元；若某台发电机未运行，则该台年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？
