题目内容
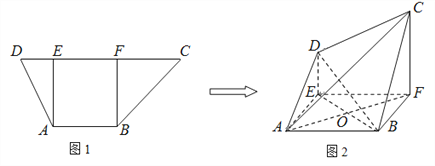
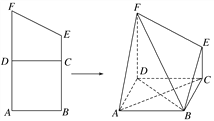
【题目】如图,梯形![]() 中,
中,![]() 且
且![]() ,沿
,沿![]() 将梯形
将梯形![]() 折起,使得平面
折起,使得平面![]() ⊥平面
⊥平面![]()
![]() .
.
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)求直线![]() 。
。
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)取BF中点为M,AC与BD交点为O,连结MO,ME,由已知结合三角形中位线定理可得四边形OCEM为平行四边形,然后利用线面平行的判定得答案;
(2)由线面垂直的性质定理可得BC⊥平面DEF,然后把三棱锥D-BEF的体积转化为三棱锥B-DEF的体积求解.
(3)分析条件得![]() ,连结
,连结![]() ,
,![]() ,由
,由![]() 求解即可.
求解即可.
试题解析:
(1)证明 如图,取BF的中点![]() ,设
,设![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() .
.
由题设知,![]() ,
,
∴![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
![]() 即
即![]() .
.
又![]() ,
,![]() ,
,
∴![]() .
.
(2)解 ∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ⊥平面
⊥平面![]() .
.
∴三棱锥![]() 的体积为
的体积为
![]() .
.
(3)∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,又
,又![]()
![]() 又
又![]() ,
,
![]()
又在正方形![]() 中
中
![]()
![]()
连结![]() ,
,![]()
![]()
![]()
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目