题目内容

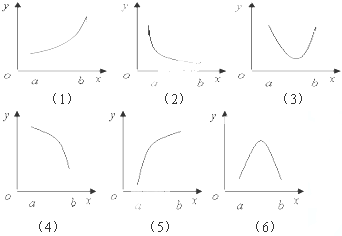若函数y=f（x）的导函数在区间[a，b]上是增函数，则函数y=f（x）在区间[a，b]上的可能图象为如图（　　）
分析：根据函数的单调性与导函数的关系，导函数大于0，函数单调递增，导函数小于0，函数单调递减，用排除法进行判断．
解答：解：∵函数y=f（x）的导函数在区间[a，b]上是增函数，
∴对任意的a＜x′＜x″＜b，有f′（a）＜f′（x′）＜f′（x″）＜f′（b），
即随着x的增大，在该点处所对应切线的斜率也应该随之增大，
∴（1）（2）（3）满足上述条件，
（4）（5）（6）即随着x的增大，在该点处所对应切线的斜率也应该随之减小，不符合题意，
故选C．
点评：本题考查了函数的单调性与导数的关系，考查了学生看图分析图的能力，要掌握函数的单调性与导函数的关系，并会观察图形，属于基础题．
练习册系列答案
相关题目
设函数f（x）=lnx-2ax．
（1）若函数y=f（x）的图象在点（1，f（1））处的切线为直线l，且直线l与圆（x+1）2+y2=1相切，求a的值；
（2）当a＞0时，求函数f（x）的单调区间．
3、若函数y=f（x）的图象关于点（h，k）对称，则函数g（x）=f（x+h）-k是（　　）
若函数y=f（x）的定义域是[0，2]，则函数F（x）=f（x+1）定义域是（　　）
若函数y=f（x）的定义域为[-2，4]，则函数g（x）=f（x）+f（-x）的定义域是
[-2，2]
[-2，2]
．
（2010•武昌区模拟）已知函数f（x）=-x3+ax2-4（a∈R）．若函数y=f（x）的图象在点P（1，f（1））处的切线的倾斜角为
π4
．
（1）求a；
（2）设f（x）的导函数是f'（x），若m，n∈[-1，1]，求f（m）+f'（n）的最小值；
（3）对实数m的值，讨论关于x的方程f（x）=m的解的个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网