题目内容
【题目】在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,x轴正半轴为极轴建立极坐标系中,直线
为极点,x轴正半轴为极轴建立极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求出线![]() 的极坐标方程及直线
的极坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 为曲线
为曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离最大值.
的距离最大值.
【答案】(1)曲线![]() 的极坐标方程
的极坐标方程![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() (2)
(2)![]()
【解析】
(1)先求解![]() 的普通方程,然后将其转化为极坐标方程;(2)设出点的参数形式,利用点到直线的距离公式以及三角函数有界性求解最大值.
的普通方程,然后将其转化为极坐标方程;(2)设出点的参数形式,利用点到直线的距离公式以及三角函数有界性求解最大值.
(1)曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),
消去方程中的![]() 可得普通方程为
可得普通方程为![]() ,
,
将![]() ,
,![]() 代入上式得
代入上式得![]() .
.
所以曲线![]() 的极坐标方程
的极坐标方程![]() .
.
直线l的极坐标方程为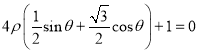 ,即
,即![]() ,
,
将![]() ,
,![]() 代人上式,得
代人上式,得![]() ,
,
所以直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)设![]() 为曲线
为曲线![]() 上任一点,
上任一点,
则点P到直线l的距离 ,
,
∴当![]() 时,
时,![]() 的最大值
的最大值![]() ,
,
∴点P到直线l的距离的最大值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.

【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:

![]()