Question

【题目】（本小题14分）

如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，E，F分别为AD，PB的中点.

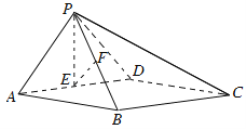
（Ⅰ）求证：PE⊥BC；

（Ⅱ）求证：平面PAB⊥平面PCD；

（Ⅲ）求证：EF∥平面PCD.

Answer 1

【答案】（Ⅰ）见解析

（Ⅱ）见解析

（Ⅲ）见解析

【解析】分析：（1）欲证，只需证明即可；（2）先证平面，再证平面PAB⊥平面PCD；（3）取中点，连接，证明，则平面.

详解：

（Ⅰ）∵，且为的中点，∴.

∵底面为矩形，∴，

∴.

（Ⅱ）∵底面为矩形，∴.

∵平面平面，∴平面.

∴.又,

∵平面，∴平面平面.

（Ⅲ）如图，取中点，连接.

∵分别为和的中点，∴，且.

∵四边形为矩形，且为的中点，

∴，

∴，且，∴四边形为平行四边形，

∴.

又平面，平面，

∴平面.