题目内容
【题目】如图，直三棱柱ABC﹣A1B1C1 ， 底面△ABC中，CA=CB=1，∠BCA=90°，棱AA1=2，M、N分别是A1B1、A1A的中点．
（1）求
的长；
（2）求cos（
）的值；
（3）求证A1B⊥C1M．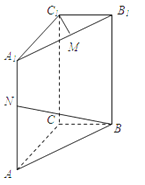
【答案】解：如图，以C为原点建立空间直角坐标系O﹣xyz．
（1）依题意得B（0，1，0），N（1，0，1），
∴|
|=
=
（2）依题意得A1（1，0，2），B（0，1，0），C（0，0，0），B1（0，1，2）．
∴
=(1,-1,2)，
=(0,1,2)，=3，||=
，||=
∴cos＜>=
=
（3）证明：依题意得C1（0，0，2），M(
,,2)
=（﹣1，1，﹣2），
=(,,0)，
∴=-+=0
∴
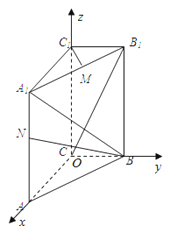
【解析】由直三棱柱ABC﹣A1B1C1中，由于BCA=90°，我们可以以C为原点建立空间直角坐标系O﹣xyz．
（1）求出B点N点坐标，代入空间两点距离公式，即可得到答案；
（2）分别求出向量 ， 的坐标，然后代入两个向量夹角余弦公式，即可得到cos＜>的值；
（3）我们求出向量 ， 的坐标，然后代入向量数量积公式，判定两个向量的数量积是否为0，若成立，则表明A1B⊥C1M.
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】某班级举行一次知识竞赛活动，活动分为初赛和决赛两个阶段，下表是初赛成绩（得分均为整数，满分为100分）的频率分布表．
分组（分数段） | 频数（人数） | 频率 |
|
| 0.16 |
| 17 |
|
| 19 | 0.38 |
|
|
|
合计 | 50 | 1 |
（Ⅰ）求频率分布表中
， 
， 
， 
的值；
（Ⅱ）决赛规则如下：参加决赛的每位同学依次口答3道判断题，答对3道题获得一等奖，答对2道题获得二等奖，答对1道题获得三等奖，否则不得奖．若某同学进入决赛，且其每次答题回答正确与否均是等可能的，试列出他回答问题的所有可能情况，并求出他至少获得二等奖的概率．
