题目内容
设m,n是异面直线,则(1)一定存在平面α,使m α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m
α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m α,n
α,n β且α⊥β。上述4个命题中正确命题的序号是( )
β且α⊥β。上述4个命题中正确命题的序号是( )
| A.(1)(2)(3) | B.(1)(2)(4) | C.(1)(3)(4) | D.(1)(4) |
C
解析试题分析:(1):将m平移到n,则此两直线相交确定一平面即符合条件,故成立;
(2):m、n不一定垂直,所以(2)不成立;
(3):过m、n公垂线段中点分别作m、n的平行线所确定平面到m、n距离就相等,(3)正确;
(4):根据空间中线面的位置关系可得满足条件的平面有无数对,故(4)正确.
故答案为:(1)(3)(4).
考点:空间中点线面的位置关系运用。
点评:本题主要考查了空间中直线与平面之间的位置关系,以及平面与平面之间的位置关系,是高考中常考的题型,属于基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )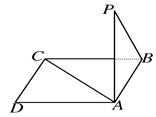
| A.90° | B.60° |
| C.45° | D.30° |
单位正方体在一个平面内的投影面积的最大值和最小值分别为( )
A.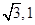 | B.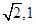 | C.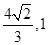 | D.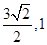 |
下列命题中,m,n表示两条不同的直线,a,b,γ表示三个不同的平面
①若m⊥a,n∥a,则m⊥n;
②若a⊥γ,b⊥γ,则a∥b;
③若m∥a,n∥a,则m∥n;
④若a∥b,b∥γ,m⊥a,则m⊥γ.
正确的命题是
| A.①③ | B.②③ | C.①④ | D.②④ |
在正方体 中,直线
中,直线 与平面
与平面 所成的角的大小为( )
所成的角的大小为( )
| A.900 | B.600 | C.450 | D.300 |
如图,正四棱锥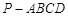 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )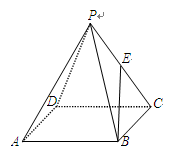
A.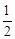 | B.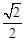 |
C.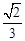 | D.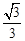 |
已知 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是
A.若 ,且 ,且 ,则 ,则 |
B.若 ,且 ,且 ,则 ,则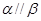 |
C.若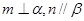 ,且 ,且 ,则 ,则 |
D.若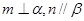 ,且 ,且 ,则 ,则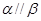 |
 是平面,
是平面,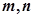 是直线,给出下列命题,其中正确的命题的个数是( )
是直线,给出下列命题,其中正确的命题的个数是( ) ,则
,则
 ,则
,则
 是异面直线,那么
是异面直线,那么 与
与 相交
相交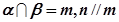 ,且
,且 ,则
,则 且
且 .
.
 则
则
 ,m、n是异面直线,那么n与α相交。
,m、n是异面直线,那么n与α相交。 ,则n//α且n//β。
,则n//α且n//β。