题目内容
如图,正四棱锥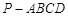 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )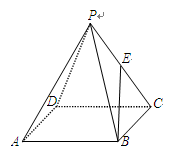
A.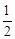 | B.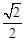 |
C.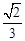 | D.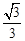 |
D
解析试题分析:由于正四棱锥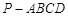 的所有棱长相等,设为2,BE=
的所有棱长相等,设为2,BE=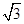 ,,EO=1,OB=
,,EO=1,OB=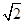 ,E为PC的中点,那么可知连接AC,BD的交点O,则将BE平移到PA,则在三角形EOB中,利用三边长度可知异面直线BE与PA所成角的余弦值是
,E为PC的中点,那么可知连接AC,BD的交点O,则将BE平移到PA,则在三角形EOB中,利用三边长度可知异面直线BE与PA所成角的余弦值是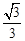 ,故选D.
,故选D.
考点:异面直线所成的角的求解
点评:求解异面直线的所成的角,一般采用平移法,放在一个三角形中来求解运算,属于基础题。

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
将正方体的纸盒展开如图,直线 、
、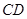 在原正方体的位置关系是( )
在原正方体的位置关系是( )
| A.平行 | B.垂直 | C.相交成60°角 | D.异面且成60°角 |
设m,n是异面直线,则(1)一定存在平面α,使m α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m
α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m α,n
α,n β且α⊥β。上述4个命题中正确命题的序号是( )
β且α⊥β。上述4个命题中正确命题的序号是( )
| A.(1)(2)(3) | B.(1)(2)(4) | C.(1)(3)(4) | D.(1)(4) |
已知m、n是两条不同的直线, 、
、 、
、 是三个不同的平面,下列命题中错误的是( )
是三个不同的平面,下列命题中错误的是( )
A.若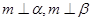 则 则 ∥ ∥ |
B.若 ∥ ∥ , , ∥ ∥ 则 则 ∥ ∥ |
C.若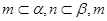 ∥n则 ∥n则 ∥ ∥ |
D.若m、n是异面直线,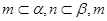 ∥ ∥ ,n∥ ,n∥ 则 则 ∥ ∥ |
下列命题:①已知直线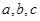 ,若
,若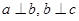 ,则
,则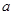 ∥
∥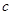 ;②
;②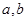 是异面直线,
是异面直线,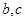 是异面直线,则
是异面直线,则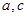 不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面
不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面 垂直;④平面
垂直;④平面 //平面
//平面 ,点
,点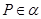 ,直线
,直线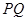 //
// ,则
,则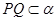 ;其中正确的命题的个数有( )
;其中正确的命题的个数有( )
| A.0 | B.1 | C.2 | D.3 |
已知 ,
, ,
,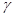 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,下列命题中正确命题是( )
是一条直线,下列命题中正确命题是( )
A.若 , , ,则 ,则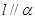 | B.若 上有两个点到 上有两个点到 的距离相等,则 的距离相等,则 |
C.若 , , ∥ ∥ ,则 ,则 | D.若 , , ,则 ,则 |
在长方体 中,
中, =2
=2 ,
, =
= ,则二面角
,则二面角 的大小是 ( )
的大小是 ( )
| A.300 | B.450 | C.600 | D.900 |
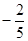
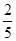
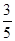
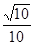
 B.
B.  C.
C. 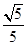 D.
D. 