题目内容
(本小题满分12分)甲、乙等五名环保志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加 岗位服务的概率;
岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,求
岗位服务的人数,求 的分布列.
的分布列.
(1)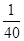 (2)
(2)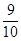 (3)
(3)
1 2 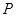
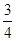
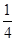
解析试题分析:(1)记甲、乙两人同时参加 岗位服务为事件
岗位服务为事件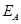 ,那么
,那么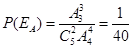 ,即甲、乙两人同时参加
,即甲、乙两人同时参加 岗位服务的概率是
岗位服务的概率是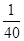 .
.
(2)记甲、乙两人同时参加同一岗位服务为事件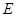 ,那么
,那么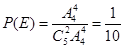 ,
,
所以,甲、乙两人不在同一岗位服务的概率是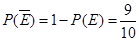 .
.
(3)随机变量 可能取的值为1,2.事件“
可能取的值为1,2.事件“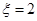 ”是指有两人同时参加
”是指有两人同时参加 岗位服务,则
岗位服务,则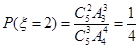 .
.
所以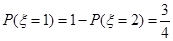 ,
, 的分布列是
的分布列是
考点:古典概型概率及随机变量分布列
1 2 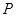
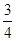
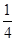
点评:在求随机变量分布列时,首先要找到随机变量可取的值,结合实际问题分析各变量值对应的事件的概率,从而得到分布列,利用分布列可求期望

练习册系列答案
相关题目
(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为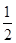 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
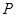 | 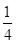 |  | 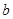 | 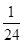 |
(2) 求
 ,
, 的值;
的值;(3) 求
 的数学期望.
的数学期望. 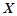 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知 .
. 的分布列及其数学期望.
的分布列及其数学期望.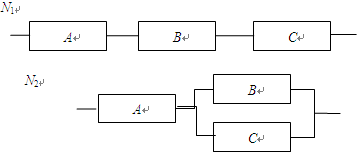
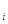 (
(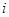 =1,2)表示方案
=1,2)表示方案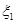 、
、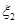 的分布列;
的分布列; ,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).