题目内容
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子里任取2个球,乙从箱子里任取1个球.若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的期望.
(1)甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大
(2)1.5
解析试题分析:(1)要想使取出的3个球颜色全不相同,则乙必须取出黄球,甲取出的两个球为一个红球一个白球,乙取出黄球的概率是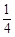 ,甲取出的两个球为一个红球一个白球的概率是
,甲取出的两个球为一个红球一个白球的概率是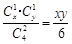 ,所以取出的3个球颜色全不相同的概率是
,所以取出的3个球颜色全不相同的概率是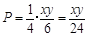 ,即甲获胜的概率为
,即甲获胜的概率为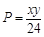 ,由
,由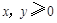 ,且
,且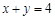 ,所以
,所以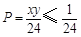
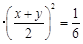 ,当
,当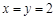 时取等号,即甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大.
时取等号,即甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大.
(2)设取出的3个球中红球的个数为ξ,则ξ的取值为0,1,2,3.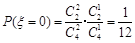 ,
,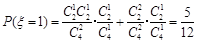 ,
,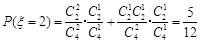 ,
,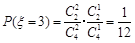 ,
,
所以取出的3个球中红球个数的期望: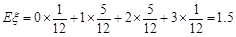 .
.
考点:本小题主要考查互斥事件的概率的求法和随机变量的分布列的数学期望的求法以及排列、组合公式的应用.
点评:随机事件的类型比较多,解决此类问题时要分清事件类型,同时要搞清楚每种事件包含几种情况,然后结合排列组合知识进行求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
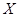 ,求
,求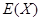 .
. ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。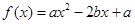 (
(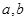
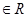 )
)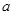 从集合
从集合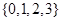 中任取一个元素,
中任取一个元素,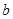 从集合
从集合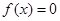 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;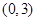 中任取一个数,
中任取一个数, 中任取一个数
中任取一个数
 表示该同学猜灯谜结束后所得奖品的总金额。
表示该同学猜灯谜结束后所得奖品的总金额。 ;
; 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者. 岗位服务的概率;
岗位服务的概率; 为这五名志愿者中参加
为这五名志愿者中参加