题目内容
18.已知集合A={y|y=x2-1,x∈R},B=$\{x|y=\sqrt{2x-4}\}$,则A∪B=[-1,+∞).分析 分别求解函数的定义域、值域得到集合A,B,然后直接利用并集运算得答案.
解答 解:∵A={y|y=x2-1,x∈R}=[-1,+∞),
B=$\{x|y=\sqrt{2x-4}\}$=[2,+∞),
∴A∪B=[-1,+∞)∪[2,+∞)=[-1,+∞).
故答案为:[-1,+∞).
点评 本题考查并集及其运算,考查了函数的定义域及其值域的求法,是基础题.

练习册系列答案
相关题目
9.若集合P={x|-1≤x<5},Q={x|x≥1},则P∩Q等于( )
| A. | {x|-1≤x<5} | B. | {x|1<x<5} | C. | {x|1≤x<5} | D. | {x|-1≤x≤1} |
6.复数${m^2}-2m+\frac{{{m^2}+m-6}}{m}i$为纯虚数,则实数m的值为( )
| A. | m≠2且m≠3 | B. | m≠2,m≠3且m≠0 | C. | m=3 | D. | 不存在 |
5.已知A={y|y=2x,x∈R},B={y|y=x2,x∈R},则A∩B=( )
| A. | {(0,0),(2,4)} | B. | {0,4} | C. | [0,+∞) | D. | R |
5.若数列{an}满足an+1=an+lg2,且a1=1,则其通项公式为( )
| A. | an=1+(n-1)lgn | B. | an=1+lgn | C. | an=1+(n-1)lg2 | D. | an=1+nlg2 |
 项和为45,前
项和为45,前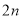 项和为60,则前
项和为60,则前 项和为( )
项和为( )