题目内容
3.已知f(x)=1nx,g(x)=x2-ax(x∈R)(1)求曲线y=f(x)于点(1,f(1)的切线方程
(2)a=3时,求函数F(x)=f(x)+g(x)单调区间
(3)设an=1+$\frac{1}{n}$(n∈N+),求证:3(a1+…an)-a12-a22…an2<1n(n+1)+2n.
分析 (1)分别求出f(1),f′(1),从而求出切线方程;
(2)将a=3代入函数F(x)的表达式,求出F′(x),从而求出函数的单调区间;
(3)根据函数的单调性得到f(1+$\frac{1}{n}$)>f(1),分别表示出代入化简后得到3(1+$\frac{1}{n}$)-${(1+\frac{1}{n})}^{2}$<2+ln(1+$\frac{1}{n}$)即3an-${{a}_{n}}^{2}$<2+ln(1+$\frac{1}{n}$),列举出各项即可得证.
解答 解:(1)∵f(x)=lnx,
∴f(1)=ln1=0,f′(x)=$\frac{1}{x}$,f′(1)=1,
∴切线方程是:y-0=x-1,
即:y=x-1;
(2)a=3时:F(x)=f(x)+g(x)=lnx+x2-3x,
∴F′(x)=$\frac{1}{x}$+2x-3=$\frac{{2x}^{2}-3x+1}{x}$=$\frac{(2x-1)(x-1)}{x}$,
令F′(x)>0,解得:x>1或0<x<$\frac{1}{2}$,令F′(x)<0,解得:$\frac{1}{2}$<x<1,
∴函数F(x)在(0,$\frac{1}{2}$),(1,+∞)递增,在($\frac{1}{2}$,1)递减;
(3)由(2)得:F(x)在(1,+∞)上是增函数.
∴F(1+$\frac{1}{n}$)>F(1)=-2,
∴ln(1+$\frac{1}{n}$)+${(1+\frac{1}{n})}^{2}$-3(1+$\frac{1}{n}$)>-2,
∴3(1+$\frac{1}{n}$)-${(1+\frac{1}{n})}^{2}$<2+ln(1+$\frac{1}{n}$),
即3an-${{a}_{n}}^{2}$<2+ln(1+$\frac{1}{n}$),
∴3a1-a12<2+ln(1+1),
3a2-${{a}_{2}}^{2}$<2+ln(1+$\frac{1}{2}$),
3a3-${{a}_{3}}^{2}$<2+ln(1+$\frac{1}{3}$),
…,
3an-${{a}_{n}}^{2}$<2+ln(1+$\frac{1}{n}$),
∴3(a1+a2+…+an)-a12-a22-…-an2
=(3a1-a12)+(3a2-a22)+…+(3an-an2)
<(2+ln$\frac{2}{1}$)+(2+ln$\frac{3}{2}$)+…+(2+ln$\frac{n+1}{n}$)
<2n+ln(n+1).
故所证不等式成立.
点评 考查学生会利用导数研究函数的单调性,会利用基本不等式求函数的最值,掌握导数在函数最值问题中的应用,是一道中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪($\frac{1+\sqrt{17}}{4}$,+∞) | C. | (-2,$\frac{1+\sqrt{17}}{4}$) | D. | (-∞,-2)∪(1,2) |
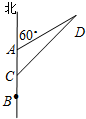 如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.