题目内容
已知函数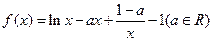 .
.
(Ⅰ)当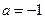 时,求曲线
时,求曲线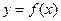 在点
在点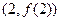 处的切线方程;
处的切线方程;
(Ⅱ)当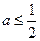 时,讨论
时,讨论 的单调性.
的单调性.
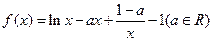 .
.(Ⅰ)当
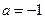 时,求曲线
时,求曲线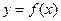 在点
在点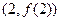 处的切线方程;
处的切线方程;(Ⅱ)当
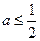 时,讨论
时,讨论 的单调性.
的单调性.解:(Ⅰ)解:当 时,
时,
所以 ,因此
,因此 ,即曲线
,即曲线 在点
在点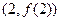 处的切线斜率为1.
处的切线斜率为1.
又 ,所以曲线
,所以曲线 在点
在点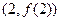 处的切线方程为
处的切线方程为
(Ⅱ)因为 ,
,
所以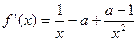
 ,
, .
.
令

①当 时,
时,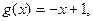
 ,
,
所以,当 时,
时, ,此时
,此时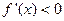 ,函数
,函数 单调递减;
单调递减;
当 时,
时, ,此时
,此时 ,函数
,函数 单调递增.
单调递增.
②当 时,由
时,由 即
即 解得
解得 .
.
(i)当 时,
时, ,
,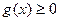 恒成立,此时
恒成立,此时 ,函数
,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;
(ii)当 时,
时, ,
, 时,
时, ,此时
,此时 ,函数
,函数 单调递减;
单调递减;
 (1,
(1, )时,
)时, ,此时
,此时 ,函数
,函数 单调递增;
单调递增;
 (
( ,
, )时,
)时, ,此时
,此时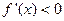 ,函数
,函数 单调递减.
单调递减.
(iii)当 时,由于
时,由于 <0,x∈(0,1)时,g(x)>0,此时
<0,x∈(0,1)时,g(x)>0,此时 ,函数
,函数 单调递减;
单调递减;
x∈(1,+∞)时, ,此时
,此时 ,函数
,函数 单调递增.
单调递增.
综上所述:
当 时,函数
时,函数 在(0,1)上单调递减;函数
在(0,1)上单调递减;函数 在(1,+∞)上单调递增;
在(1,+∞)上单调递增;
当 时,函数
时,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;
当 时,函数
时,函数 在(0,1)上单调递减;函数
在(0,1)上单调递减;函数 在(1,
在(1, )上单调递增;函数
)上单调递增;函数 在(
在( ,+∞)上单调递减.
,+∞)上单调递减.
 时,
时,
所以
 ,因此
,因此 ,即曲线
,即曲线 在点
在点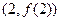 处的切线斜率为1.
处的切线斜率为1.又
 ,所以曲线
,所以曲线 在点
在点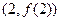 处的切线方程为
处的切线方程为
(Ⅱ)因为
 ,
,所以
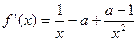
 ,
, .
.令


①当
 时,
时,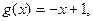
 ,
,所以,当
 时,
时, ,此时
,此时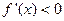 ,函数
,函数 单调递减;
单调递减;当
 时,
时, ,此时
,此时 ,函数
,函数 单调递增.
单调递增.②当
 时,由
时,由 即
即 解得
解得 .
.(i)当
 时,
时, ,
,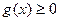 恒成立,此时
恒成立,此时 ,函数
,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;(ii)当
 时,
时, ,
, 时,
时, ,此时
,此时 ,函数
,函数 单调递减;
单调递减; (1,
(1, )时,
)时, ,此时
,此时 ,函数
,函数 单调递增;
单调递增; (
( ,
, )时,
)时, ,此时
,此时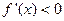 ,函数
,函数 单调递减.
单调递减.(iii)当
 时,由于
时,由于 <0,x∈(0,1)时,g(x)>0,此时
<0,x∈(0,1)时,g(x)>0,此时 ,函数
,函数 单调递减;
单调递减;x∈(1,+∞)时,
 ,此时
,此时 ,函数
,函数 单调递增.
单调递增.综上所述:
当
 时,函数
时,函数 在(0,1)上单调递减;函数
在(0,1)上单调递减;函数 在(1,+∞)上单调递增;
在(1,+∞)上单调递增;当
 时,函数
时,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;当
 时,函数
时,函数 在(0,1)上单调递减;函数
在(0,1)上单调递减;函数 在(1,
在(1, )上单调递增;函数
)上单调递增;函数 在(
在( ,+∞)上单调递减.
,+∞)上单调递减.
练习册系列答案
相关题目
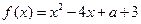 ,
,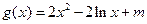
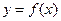 在[-1,1]上存在零点,求实数
在[-1,1]上存在零点,求实数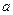 的取值范围;
的取值范围;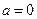 时,若对任意的
时,若对任意的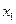 ∈[1,4],总存在
∈[1,4],总存在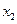 ∈[1,4],使
∈[1,4],使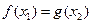 成立,求实数
成立,求实数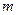 的取值范围;
的取值范围;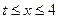 )的值域为区间D,是否存在常数
)的值域为区间D,是否存在常数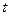 ,使区间D的长度为
,使区间D的长度为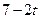 ?若存在,求出
?若存在,求出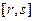 的长度为
的长度为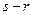 ).
).
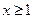 时, 证明: 不等式
时, 证明: 不等式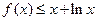 恒成立;
恒成立; 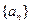 满足
满足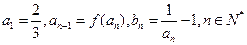 ,证明数列
,证明数列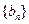 是等比数列,并求出数列
是等比数列,并求出数列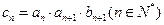 ,证明:
,证明: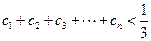 .
.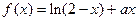 在点
在点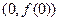 处的切线斜率为
处的切线斜率为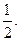
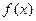 的极值;
的极值;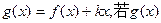 在(-∞,1)上是增函数,求实数
在(-∞,1)上是增函数,求实数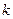 的取值范围;
的取值范围;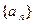 满足
满足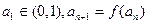 ,求证:对一切
,求证:对一切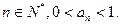
 ,若
,若 在R上可导,则
在R上可导,则 = 。
= 。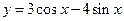 的导数为 .
的导数为 .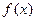 的导函数为
的导函数为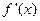 ,且满足
,且满足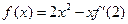 ,则
,则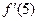 = .
= . 则a的值等于 ( )
则a的值等于 ( )



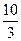
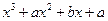 在x=1处取得极值(a>0)
在x=1处取得极值(a>0)