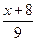题目内容
(本小题满分14分)
已知曲线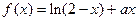 在点
在点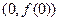 处的切线斜率为
处的切线斜率为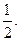
(1)求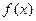 的极值;
的极值;
(2)设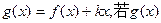 在(-∞,1)上是增函数,求实数
在(-∞,1)上是增函数,求实数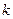 的取值范围;
的取值范围;
(3)若数列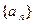 满足
满足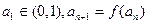 ,求证:对一切
,求证:对一切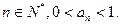
已知曲线
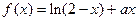 在点
在点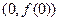 处的切线斜率为
处的切线斜率为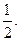
(1)求
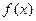 的极值;
的极值;(2)设
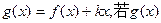 在(-∞,1)上是增函数,求实数
在(-∞,1)上是增函数,求实数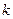 的取值范围;
的取值范围;(3)若数列
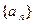 满足
满足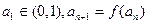 ,求证:对一切
,求证:对一切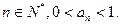
(1)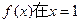 处取得极大值1,无极小值。
处取得极大值1,无极小值。
(2)实数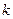 的取值范围是
的取值范围是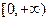
(3)略
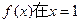 处取得极大值1,无极小值。
处取得极大值1,无极小值。(2)实数
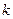 的取值范围是
的取值范围是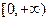
(3)略
解:(1)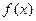 的定义域是
的定义域是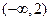 …………1分
…………1分
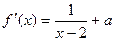 …………2分
…………2分
由题知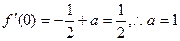
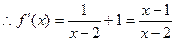
令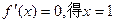 …………3分
…………3分
当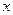 变化时,
变化时,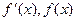 的变化情况如下表所示
的变化情况如下表所示
所以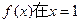 处取得极大值1,无极小值。…………5分
处取得极大值1,无极小值。…………5分
(2)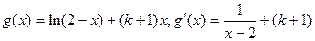 …………6分
…………6分
由题知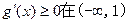 上恒成立,即
上恒成立,即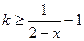 在(-∞,1)上恒成立……7分
在(-∞,1)上恒成立……7分
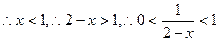
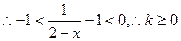
即实数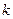 的取值范围是
的取值范围是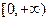 …………9分
…………9分
(3)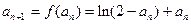
(i)当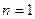 时,由题意知
时,由题意知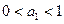 …………11分
…………11分
(ii)假设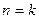 时,有
时,有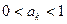 ,则
,则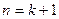 时,
时,
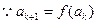
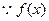 在(0,1)上是增函数,
在(0,1)上是增函数,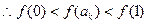
即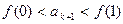 ,即
,即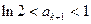 ,又
,又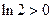
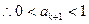
即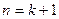 时,求证的结论也成立
时,求证的结论也成立
由(i)(ii)可知对一切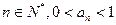 …………14分
…………14分
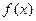 的定义域是
的定义域是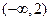 …………1分
…………1分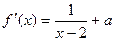 …………2分
…………2分由题知
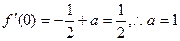
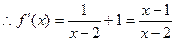
令
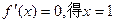 …………3分
…………3分当
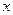 变化时,
变化时,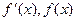 的变化情况如下表所示
的变化情况如下表所示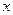 |  | 1 | (1,2) |
 | + | 0 | - |
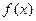 |  | 1 |  |
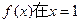 处取得极大值1,无极小值。…………5分
处取得极大值1,无极小值。…………5分(2)
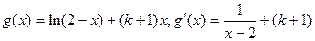 …………6分
…………6分由题知
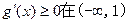 上恒成立,即
上恒成立,即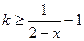 在(-∞,1)上恒成立……7分
在(-∞,1)上恒成立……7分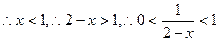
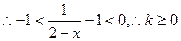
即实数
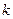 的取值范围是
的取值范围是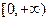 …………9分
…………9分(3)
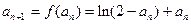
(i)当
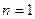 时,由题意知
时,由题意知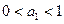 …………11分
…………11分(ii)假设
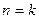 时,有
时,有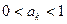 ,则
,则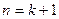 时,
时,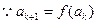
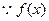 在(0,1)上是增函数,
在(0,1)上是增函数,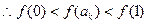
即
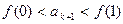 ,即
,即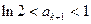 ,又
,又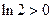
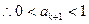
即
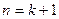 时,求证的结论也成立
时,求证的结论也成立由(i)(ii)可知对一切
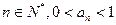 …………14分
…………14分
练习册系列答案
相关题目
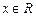 ,函数
,函数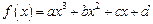 在
在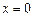 处取得极值,曲线
处取得极值,曲线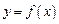 过原点
过原点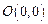 和点
和点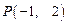 .若曲线
.若曲线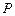 处的切线
处的切线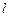 与直线
与直线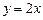 的夹角为
的夹角为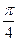 ,且直线
,且直线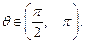 (Ⅰ)求
(Ⅰ)求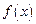 的解析式;(Ⅱ)若函数
的解析式;(Ⅱ)若函数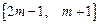 上是增函数,求实数
上是增函数,求实数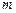 的取值范围;(Ⅲ)若
的取值范围;(Ⅲ)若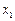 、
、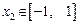 ,求证:
,求证: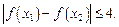
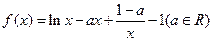 .
.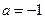 时,求曲线
时,求曲线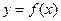 在点
在点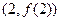 处的切线方程;
处的切线方程;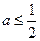 时,讨论
时,讨论 的单调性.
的单调性.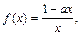
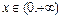 设0<
设0<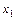 <
<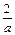 ,记曲线y=
,记曲线y=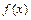 在点
在点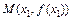 处的切线为L,
处的切线为L,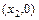 ,证明:①
,证明:①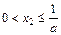 ; ②若
; ②若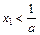 ,则
,则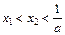 。
。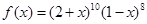 ,则
,则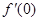 的值为( )
的值为( )


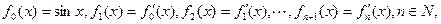 则
则 ▲ .
▲ .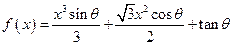 (
(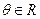 ),则导数值
),则导数值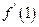 的取值范围是 _________.
的取值范围是 _________.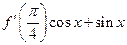 ,则
,则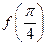 的值为
的值为 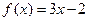 ,则
,则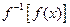 等于( )
等于( )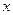 (B)
(B) 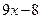 (C)
(C) 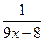 (D)
(D)