题目内容
已知双曲线的焦点是(±
,0),渐近线方程为y=±
x,则双曲线的两条准线间的距离为 .
| 26 |
| 3 |
| 2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据双曲线的渐近线方程焦点坐标设出双曲线的方程,求出双曲线中的c,再根据双曲线的焦点坐标求出参数的值,得到双曲线的方程,
再由双曲线方程求出准线方程,最后计算两准线间距离.
再由双曲线方程求出准线方程,最后计算两准线间距离.
解答:
解:∵双曲线的两条渐近线的方程为:y=±
x,一个焦点为F1(-
,0),
∴设双曲线方程为
-
=1(λ>0)
则双曲线中a2=4λ,b2=9λ,
∴c2=a2+b2=4λ+9λ=13λ
又∵一个焦点为F1(-
,0),
∴c=
,
∴13λ=26,λ=2.
∴双曲线方程为
-
=1
∴准线方程为x=±
=±
=±
∴两准线间距离为:
.
故答案为:
.
| 3 |
| 2 |
| 26 |
∴设双曲线方程为
| x2 |
| 4λ |
| y2 |
| 9λ |
则双曲线中a2=4λ,b2=9λ,
∴c2=a2+b2=4λ+9λ=13λ
又∵一个焦点为F1(-
| 26 |
∴c=
| 26 |
∴13λ=26,λ=2.
∴双曲线方程为
| x2 |
| 8 |
| y2 |
| 18 |
∴准线方程为x=±
| a2 |
| c |
| 8 | ||
|
4
| ||
| 13 |
∴两准线间距离为:
| 8 |
| 13 |
| 26 |
故答案为:
| 8 |
| 13 |
| 26 |
点评:本题主要考查了双曲线的标准方程及其几何性质,待定系数法求双曲线的标准方程,双曲线的渐近线、准线、焦点坐标间的关系

练习册系列答案
相关题目

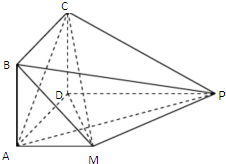 如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=