题目内容
已知P是椭圆
+y2=1上的一点,F1、F2为椭圆的左、右焦点.
(1)当∠F1PF2=60°时,求△PF1F2的面积;
(2)当∠F1PF2为钝角时,求点P的横坐标的取值范围.
| x2 |
| 4 |
(1)当∠F1PF2=60°时,求△PF1F2的面积;
(2)当∠F1PF2为钝角时,求点P的横坐标的取值范围.
考点:椭圆的简单性质
专题:计算题,解三角形,圆锥曲线的定义、性质与方程
分析:(1)运用椭圆的定义和余弦定理及面积公式,即可求得;
(2)设p(x,y),根据椭圆方程求得两焦点坐标,根据∠F1PF2是钝角推断出PF12+PF22<F1F22代入p坐标求得x和y的不等式关系,求得x的范围.
(2)设p(x,y),根据椭圆方程求得两焦点坐标,根据∠F1PF2是钝角推断出PF12+PF22<F1F22代入p坐标求得x和y的不等式关系,求得x的范围.
解答:
(1)解:∵椭圆的方程为
+y2=1,
∴a=2,b=1,c=
.
又∵P为椭圆上一点,∠F1PF2=60°,F1、F2为左右焦点,
∴|F1P|+|PF2|=2a=4,|F1F2|=2
,
∴|F1F2|2=(|PF1|+|PF2|)2-2|F1P||PF2|-2|F1P|•|PF2|cos60°
=16-3|F1P|•|PF2|=12,
∴|F1P|•|PF2|=
.
∴S△PF1F2=
|F1P|•|PF2|sin60°
=
×
×
=
;
(2)设p(x,y),则 F1(-
,0),F2(
,0),
且∠F1PF2是钝角,PF12+PF22<F1F22即(x+
)2+y2+(x-
)2+y2<12,
?x2+3+y2<6,即x2+(1-
)<3即x2<
.即-
<x<
.
故点P的横坐标的取值范围(-
,
).
| x2 |
| 4 |
∴a=2,b=1,c=
| 3 |
又∵P为椭圆上一点,∠F1PF2=60°,F1、F2为左右焦点,
∴|F1P|+|PF2|=2a=4,|F1F2|=2
| 3 |
∴|F1F2|2=(|PF1|+|PF2|)2-2|F1P||PF2|-2|F1P|•|PF2|cos60°
=16-3|F1P|•|PF2|=12,
∴|F1P|•|PF2|=
| 4 |
| 3 |
∴S△PF1F2=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 4 |
| 3 |
| ||
| 2 |
| ||
| 3 |
(2)设p(x,y),则 F1(-
| 3 |
| 3 |
且∠F1PF2是钝角,PF12+PF22<F1F22即(x+
| 3 |
| 3 |
?x2+3+y2<6,即x2+(1-
| x2 |
| 4 |
| 8 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
故点P的横坐标的取值范围(-
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题主要考查了椭圆的定义和方程及简单性质和解不等式,考查余弦定理和面积公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,且a2=4,S2=6,若bn=
,则数列{bn}的前n项和Tn为( )
| 1 |
| Sn |
A、
| ||
B、
| ||
C、
| ||
D、
|
 截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:
截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解我地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:
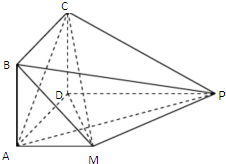 如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=