题目内容
在平面直角坐标系xOy中,点A在圆x2+y2-2ax=0(a≠0)上,M点满足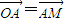 ,M点的轨迹为曲线C.
,M点的轨迹为曲线C.(I)求曲线C的方程;
(II)若直线y=x-1与曲线C交于P、Q两点,且
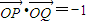 ,求a的值.
,求a的值.
【答案】分析:(I)根据向量关系,可得M与A坐标之间的关系,利用点A在圆x2+y2-2ax=0(a≠0)上,即可求得曲线C的方程;
(II)将直线y=x-1与曲线C联立,利用韦达定理及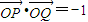 ,建立方程,即可求a的值
,建立方程,即可求a的值
解答:解:(I)设M(x,y),A(x,y)
∵M点满足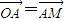 ,
,
∴(x,y)=(x-x,y-y)
∴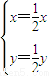
∵点A在圆x2+y2-2ax=0(a≠0)上
∴( x)2+(
x)2+( y)2-2a×
y)2-2a× x=0(a≠0)
x=0(a≠0)
∴曲线C的方程为x2+y2-4ax=0(a≠0);
(II)设P(x1,y1),Q(x2,y2)
将直线y=x-1代入x2+y2-4ax=0,整理得2x2-2(2a+1)x+1=0
∴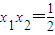 ,x1+x2=2a+1
,x1+x2=2a+1
∴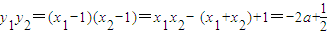
∵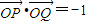 ,
,
∴x1x2+y1y2=-1
∴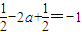
∴a=1.
当a=1时,△=62-8>0
∴a的值为1.
点评:本题重点考查轨迹方程,考查直线与圆的位置关系,考查向量知识的运用,解题的关键是确定动点坐标之间的关系,将向量关系转化为坐标之间的关系.
(II)将直线y=x-1与曲线C联立,利用韦达定理及
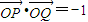 ,建立方程,即可求a的值
,建立方程,即可求a的值解答:解:(I)设M(x,y),A(x,y)
∵M点满足
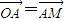 ,
,∴(x,y)=(x-x,y-y)
∴
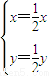
∵点A在圆x2+y2-2ax=0(a≠0)上
∴(
 x)2+(
x)2+( y)2-2a×
y)2-2a× x=0(a≠0)
x=0(a≠0)∴曲线C的方程为x2+y2-4ax=0(a≠0);
(II)设P(x1,y1),Q(x2,y2)
将直线y=x-1代入x2+y2-4ax=0,整理得2x2-2(2a+1)x+1=0
∴
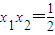 ,x1+x2=2a+1
,x1+x2=2a+1∴
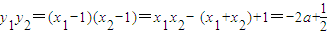
∵
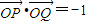 ,
,∴x1x2+y1y2=-1
∴
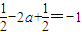
∴a=1.
当a=1时,△=62-8>0
∴a的值为1.
点评:本题重点考查轨迹方程,考查直线与圆的位置关系,考查向量知识的运用,解题的关键是确定动点坐标之间的关系,将向量关系转化为坐标之间的关系.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是