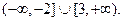题目内容
已知两个命题r(x):sinx+cosx>m,s(x):x2+mx+1>0.如果对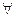 x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
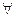 x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.实数m的取值范围是m≤-2或-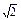 ≤m<2
≤m<2
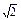 ≤m<2
≤m<2∵sinx+cosx=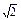 sin(x+
sin(x+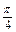 )≥-
)≥-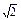 ,
,
∴当r(x)是真命题时,m<-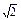 3分
3分
又∵对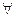 x∈R,s(x)为真命题,即x2+mx+1>0恒成立,
x∈R,s(x)为真命题,即x2+mx+1>0恒成立,
有Δ=m2-4<0,∴-2<m<2. 6分
∴当r(x)为真,s(x)为假时,m<-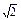 ,
,
同时m≤-2或m≥2,即m≤-2; 9分
当r(x)为假,s(x)为真时,m≥-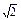 且-2<m<2,
且-2<m<2,
即-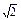 ≤m<2. 12分
≤m<2. 12分
综上,实数m的取值范围是m≤-2或-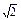 ≤m<2. 14分
≤m<2. 14分
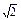 sin(x+
sin(x+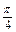 )≥-
)≥-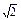 ,
,∴当r(x)是真命题时,m<-
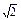 3分
3分又∵对
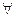 x∈R,s(x)为真命题,即x2+mx+1>0恒成立,
x∈R,s(x)为真命题,即x2+mx+1>0恒成立,有Δ=m2-4<0,∴-2<m<2. 6分
∴当r(x)为真,s(x)为假时,m<-
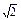 ,
,同时m≤-2或m≥2,即m≤-2; 9分
当r(x)为假,s(x)为真时,m≥-
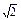 且-2<m<2,
且-2<m<2,即-
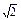 ≤m<2. 12分
≤m<2. 12分综上,实数m的取值范围是m≤-2或-
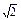 ≤m<2. 14分
≤m<2. 14分
练习册系列答案
相关题目
 不能作除数;
不能作除数;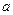 ,
,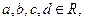 若
若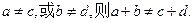
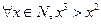
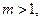 则方程
则方程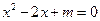 无实数根。
无实数根。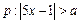 和条件
和条件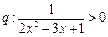 ,现在要选择适当的实数
,现在要选择适当的实数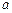 的值,分别利用所给的两上条件作为
的值,分别利用所给的两上条件作为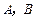 构造命题:“若
构造命题:“若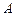 则
则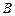 ”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.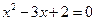 ,则
,则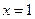 或
或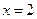 ;②若
;②若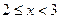 ,则
,则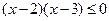 ;
;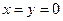 ,则
,则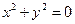 ;
;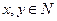 ,且
,且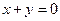 是奇数,则
是奇数,则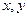 中一个是奇数,一个是偶数,那么( ).
中一个是奇数,一个是偶数,那么( ).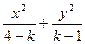 =1,给出下面四个命题:
=1,给出下面四个命题: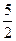
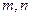 是两条不同的直线,
是两条不同的直线,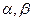 是两个不同的平面,给出下列四个命题:
是两个不同的平面,给出下列四个命题: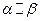 ,
,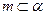 ,则
,则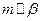 ; 2)若
; 2)若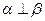 ,
,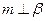 ;
;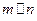 ,
,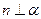 ,则
,则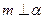 ;4)若
;4)若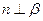 ,
,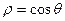 与直线
与直线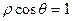 相切;
相切; 的参数方程为
的参数方程为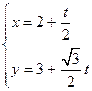
 为参数),则它的倾斜角为
为参数),则它的倾斜角为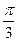 ;
;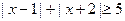 的解集为
的解集为