题目内容
11．设f（x）是定义在R上周期为2的偶函数，当x∈[0，1]时，f（x）=x，若在区间（-2，+∞）内，函数h（x）=f（x）-loga（x+2）恰有3个零点，则a的取值范围是（ ）| A． | （1，3） | B． | （2，4） | C． | （3，5） | D． | （5，7） |
分析 函数h（x）=f（x）-loga（x+2）恰有3个零点可化为函数f（x）与函数y=loga（x+2）恰有3个交点，作图象求解即可．
解答 解：函数h（x）=f（x）-loga（x+2）恰有3个零点可化为
函数f（x）与函数y=loga（x+2）恰有3个交点，
作函数f（x）与函数y=loga（x+2）的图象如下，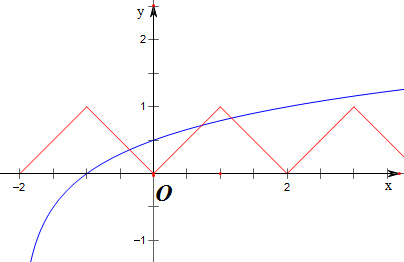
结合图象可知，
$\left\{\begin{array}{l}{0＜lo{g}_{a}（2+1）＜1}\\{lo{g}_{a}（2+3）＞1}\end{array}\right.$；
解得，3＜a＜5；
故选C．
点评 本题考查了函数的零点与函数的图象的关系应用，属于基础题．
练习册系列答案
相关题目
6．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点分别为F1，F2渐近线分别为l1，l2，位于第一象限的点P在l1上，若l2⊥PF1，l2∥PF2，则双曲线的离心率是（ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{2}$ |
3．一个几何体的三视图如图所示，则该几何体的体积的是（ ）
| A． | $\frac{47}{6}$ | B． | $\frac{23}{3}$ | C． | $\frac{15}{2}$ | D． | 7 |
20．
设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，（a＞0，b＞0）的左焦点F（-c，0），则x2+y2=c2与双曲线的一条渐近线交于点A，直线AF交另一条渐近线与点B．若$\overrightarrow{FB}$=$\frac{1}{2}$$\overrightarrow{FA}$，则双曲线的离心率为（ ）
设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，（a＞0，b＞0）的左焦点F（-c，0），则x2+y2=c2与双曲线的一条渐近线交于点A，直线AF交另一条渐近线与点B．若$\overrightarrow{FB}$=$\frac{1}{2}$$\overrightarrow{FA}$，则双曲线的离心率为（ ）| A． | 2 | B． | 3 | C． | $\frac{3}{2}$ | D． | $\frac{\sqrt{5}+1}{2}$ |
1．已知抛物线y2=2px（p＞0）的焦点F恰好是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点，两条曲线的交点的连线过点F，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 1+$\sqrt{2}$ | D． | 1+$\sqrt{3}$ |