题目内容
【题目】如图所示,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH. 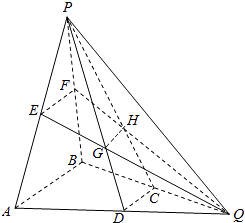
(1)求证:AB∥GH;
(2)求二面角D﹣GH﹣E的余弦值.
【答案】
(1)证明:如图,
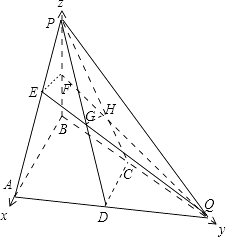
∵C,D为AQ,BQ的中点,∴CD∥AB,
又E,F分别AP,BP的中点,∴EF∥AB,
则EF∥CD.又EF平面EFQ,∴CD∥平面EFQ.
又CD平面PCD,且平面PCD∩平面EFQ=GH,∴CD∥GH.
又AB∥CD,∴AB∥GH
(2)解:由AQ=2BD,D为AQ的中点可得,三角形ABQ为直角三角形,
以B为坐标原点,分别以BA、BQ、BP所在直线为x、y、z轴建立空间直角坐标系,
设AB=BP=BQ=2,
则D(1,1,0),C(0,1,0),E(1,0,1),F(0,0,1),
因为H为三角形PBQ的重心,所以H(0, ![]() ,
, ![]() ).
).
则 ![]() ,
, ![]()
![]() ,
, ![]() .
.
设平面GCD的一个法向量为 ![]()
由 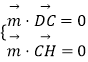 ,得
,得 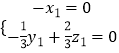 ,取z1=1,得y1=2.
,取z1=1,得y1=2.
所以 ![]() .
.
设平面EFG的一个法向量为 ![]()
由 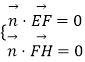 ,得
,得 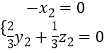 ,取z2=2,得y2=1.
,取z2=2,得y2=1.
所以 ![]() .
.
所以 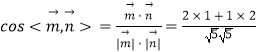 =
= ![]() .
.
则二面角D﹣GH﹣E的余弦值等于- ![]()
【解析】(1)由给出的D,C,E,F分别是AQ,BQ,AP,BP的中点,利用三角形中位线知识及平行公理得到DC平行于EF,再利用线面平行的判定和性质得到DC平行于GH,从而得到AB∥GH;(2)由题意可知BA、BQ、BP两两相互垂直,以B为坐标原点建立空间直角坐标系,设出BA、BQ、BP的长度,标出点的坐标,求出一些向量的坐标,利用二面角的两个面的法向量所成的角的余弦值求解二面角D﹣GH﹣E的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的性质的相关知识,掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.

 黄冈创优卷系列答案
黄冈创优卷系列答案