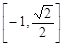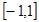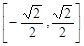题目内容
已知函数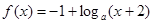 (a>0,且a≠1),
(a>0,且a≠1),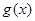 =
= .
.
(1)函数 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标;
(2)若函数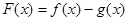 的图像过点(2,
的图像过点(2,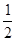 ),证明:函数
),证明:函数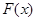 在
在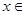 (1,2)上有唯一的零点.
(1,2)上有唯一的零点.
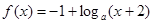 (a>0,且a≠1),
(a>0,且a≠1),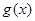 =
= .
.(1)函数
 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标;(2)若函数
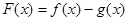 的图像过点(2,
的图像过点(2,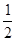 ),证明:函数
),证明:函数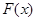 在
在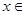 (1,2)上有唯一的零点.
(1,2)上有唯一的零点. (1)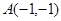
(2)先利用已知条件求出a,在利用单调性和零点存在定理即可证明
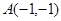
(2)先利用已知条件求出a,在利用单调性和零点存在定理即可证明
试题分析:(1)因为对数函数
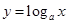 恒过顶点(1,0),
恒过顶点(1,0),所以令
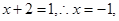 所以过顶点
所以过顶点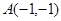 5分
5分(2)∵
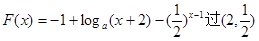
∴代入计算可得a=2 7分
∴
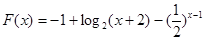
 上的增函数和减函数
上的增函数和减函数∴
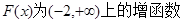
∴
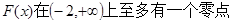 10分
10分又(1,2)
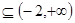
∴
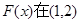 上至多有一个零点. 12分
上至多有一个零点. 12分而
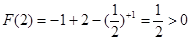
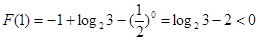
∴函数
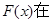 (1,2)
(1,2) 16分
16分点评:指数函数和对数函数都过定点,这条性质要灵活应用;利用函数的零点存在定理时要注意它只能判断有零点,不能判断零点的个数.

练习册系列答案
相关题目
 对应密文:
对应密文: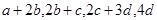 ,当接收方收到密文14,9,23,28时,解密得到的明文为( )
,当接收方收到密文14,9,23,28时,解密得到的明文为( )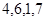
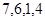
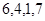
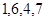
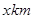 ,建在C处的垃圾处理厂对城A和城B的总影响度为
,建在C处的垃圾处理厂对城A和城B的总影响度为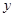 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。

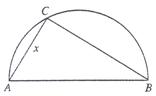
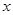 的函数;
的函数; (2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。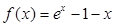
 在点
在点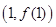 处的切线方程;
处的切线方程;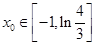 ,满足
,满足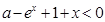 成立,求
成立,求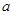 的取值范围;
的取值范围;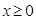 时,
时,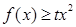 恒成立,求
恒成立,求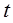 的取值范围.
的取值范围.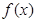 小时,写出
小时,写出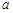 使
使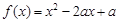 的定义域为
的定义域为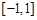 ,值域为
,值域为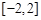 ?若存在,求出
?若存在,求出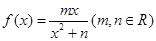 在点(1,f(1))处的切线方程为y = 2.
在点(1,f(1))处的切线方程为y = 2.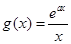 若对任意的
若对任意的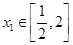 ,总存唯一实数
,总存唯一实数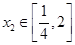 ,使得
,使得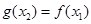 ,求实数a的取值范围.
,求实数a的取值范围. 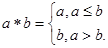 如
如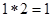 ,则函数
,则函数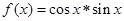 的值域为( )
的值域为( )