题目内容
已知数列 的前
的前 项和为
项和为 满足
满足 ,且
,且 .
.
(1)试求出 的值;
的值;
(2)根据 的值猜想出
的值猜想出 关于
关于 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.
(1)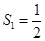 ,
, ,
,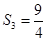 ;(2)猜想:
;(2)猜想: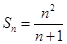 ,证明详见解析.
,证明详见解析.
解析试题分析:本试题主要考查数列的前 项的求解和数学归纳法的综合运用.(1)运用赋值的思想得出
项的求解和数学归纳法的综合运用.(1)运用赋值的思想得出 ;(2)先由求出的几项
;(2)先由求出的几项 与序号的关系,猜想
与序号的关系,猜想 的表达式,进而运用数学归纳法来分两步证明,注意证明要用到假设.
的表达式,进而运用数学归纳法来分两步证明,注意证明要用到假设.
(1)依条件可知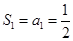
而当 时有
时有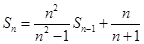
所以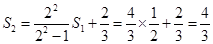 ,
, 3分
3分
(2)因为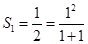 ,
,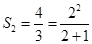 ,
,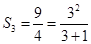 ,故可猜想
,故可猜想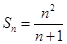 5分
5分
①当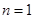 时,左边
时,左边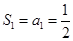 ,右边
,右边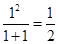 ,故等式成立 7分
,故等式成立 7分
②假设 时,
时,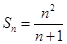 成立,即
成立,即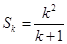 8分
8分
则当 时,
时,
左边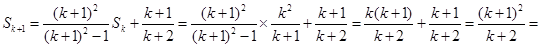 右边
右边
所以当 时,等式
时,等式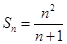 也成立 11分
也成立 11分
由①②可知,对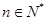 ,等式
,等式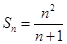 成立 12分.
成立 12分.
考点:1.数列的递推关系式;2.数学归纳法.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 的前
的前 项和
项和 ,则
,则 =
=  (n∈N*).
(n∈N*). ,计算a2,a3,a4的值,并求出数列{an}的通项公式.
,计算a2,a3,a4的值,并求出数列{an}的通项公式. 的前
的前 项和为
项和为 ,满足
,满足 ,
, ,且
,且 .
. 、
、 、
、 的值;
的值; 的通项公式.
的通项公式. 前
前 项和
项和 ,
,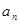 ;(2)若它的第
;(2)若它的第 项满足
项满足 ,求
,求 满足
满足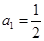 ,
, .
. 的值,由此猜测
的值,由此猜测 .
. 的首项
的首项 ,公差
,公差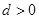 ,且第
,且第 项、第
项、第 项、第
项、第 项分别是等比数列
项分别是等比数列 的第
的第 项、第
项、第 项.
项. 对任意
对任意 ,均有
,均有 成立.
成立. ; ②求
; ②求 .
. 前n项和
前n项和 =
= (
(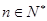 ), 数列
), 数列 为等比数列,首项
为等比数列,首项 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足 ,
, ,
, 为等比数列.
为等比数列. ,记数列
,记数列