题目内容
数列{an}中,an>0,an≠1,且 (n∈N*).
(n∈N*).
(1)证明:an≠an+1;
(2)若 ,计算a2,a3,a4的值,并求出数列{an}的通项公式.
,计算a2,a3,a4的值,并求出数列{an}的通项公式.
(1)祥见解析;(2)
解析试题分析:(1)利用反证法,若an+1=an,即 ,解得 an=0或1,结论与题干条件矛盾;(2)法一:根据
,解得 an=0或1,结论与题干条件矛盾;(2)法一:根据 ,
, ,求出
,求出 ,
, ,
, ,,观察各项分子通项为3n-1,分母通项为3n-1+1,于是可以写出通项公式an,进而可用数学归纳法加以证明.法二:由
,,观察各项分子通项为3n-1,分母通项为3n-1+1,于是可以写出通项公式an,进而可用数学归纳法加以证明.法二:由 (n∈N*),取倒数得
(n∈N*),取倒数得 ,从而可转化为:
,从而可转化为: 这样就可选求出等比数列
这样就可选求出等比数列 是以
是以 为首项,
为首项, 为公比,从而可写出其通项公式,进而就可求出数列{an}的通项公式.
为公比,从而可写出其通项公式,进而就可求出数列{an}的通项公式.
试题解析:(1)证明:(反证法)若an=an+1,则由 (n∈N*),得
(n∈N*),得 ,
,
得an=1,这与已知an≠1相悖,故an≠an+1. 4分
(2)方法一:(举例-猜想-证明)
若 ,由
,由 (n∈N*)得,
(n∈N*)得, ,
, ,
, ,猜想:
,猜想: (n∈N*), 8分
(n∈N*), 8分
以下用数学归纳法证明:
①当n=1时, ,所以当n=1时命题成立; 9分
,所以当n=1时命题成立; 9分
②假设当n=k时,命题成立,即 ,
,
则当n=k+1时, , 12分
, 12分
所以,当n=k+1时,命题也成立,故 (n∈N*), 13分
(n∈N*), 13分
由①、②可知,对所有的自然数n,都有 (n∈N*). 14分
(n∈N*). 14分
(说明:其它方法请相应给分)
方法二:(利用数列递推关系求通项公式)
由 (n∈N*),取倒数得
(n∈N*),取倒数得 ,
,
又 ,令2+3t=t,解得t=-1,
,令2+3t=t,解得t=-1,
∴ ,
,
∴ 是以
是以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
∴ ,∴
,∴ ,∴
,∴ .
.
考点:1.反正法;2.数列递推式;3.数学归纳法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
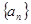 、
、 的前
的前 项和分别为
项和分别为 、
、 ,且满足
,且满足 ,则
,则 的值为 ________.
的值为 ________. 的前
的前 项和
项和 ,则
,则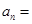 .
. 中,
中,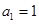 ,
, ,其通项公式
,其通项公式 = .
= . 中,
中, ,其中
,其中 。
。 的值;
的值;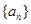 的前n项和
的前n项和 满足
满足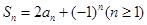
 、
、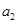 、
、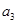 ;
;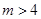 有
有
 的前
的前 项和为
项和为 满足
满足 ,且
,且 .
. 的值;
的值;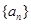 中,
中,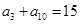 ,且
,且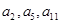 成等比数列.
成等比数列.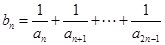 ,证明:
,证明: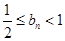 .
. 满足
满足 ,则
,则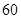 项和为
项和为