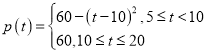题目内容
【题目】如图,在四棱锥P-ABCD中,在底面ABCD中,AD//BC,AD⊥CD,Q是AD的中点,M是棱PC的中点,PA=PD=2,BC=![]() AD=1,CD=
AD=1,CD=![]() ,PB=
,PB=![]() .
.
(Ⅰ)求证:平面PAD⊥底面ABCD;
(Ⅱ)试求三棱锥B-PQM的体积.

【答案】(1)证明:∵![]() ,
,![]() ,
,![]() 是
是![]() 的中点,∴四边形
的中点,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() .∵
.∵![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,
,![]() 是
是![]() 的中点,故
的中点,故![]() .
.
又![]() ,由勾股定理得
,由勾股定理得![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() ,∴平面
,∴平面![]() 底面
底面![]() ;
;
(2)![]()
【解析】
(Ⅰ)若证面面垂直,则需证线面垂直,根据平行线的性质证明垂直,由勾股定理也可证垂直,定理可证明面面垂直.
(Ⅱ)通过垂直关系证明线与底面垂直,确定高线,由中点性质,先求出大的三棱锥体积再乘以![]() 即可.
即可.
(Ⅰ)证明:∵![]() ,
,![]() ,
,![]() 是
是![]() 的中点,∴四边形
的中点,∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .∵
.∵![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,
,![]() 是
是![]() 的中点,故
的中点,故![]() .
.
又![]() ,由勾股定理得
,由勾股定理得![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() ,∴平面
,∴平面![]() 底面
底面![]() .
.
(Ⅱ)∵![]() ,
,![]() 是
是![]() 的中点,∴
的中点,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 是
是![]() 的中点,
的中点,
故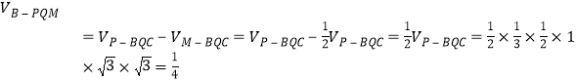

【题目】一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转速度而变化,下表为抽样试验的结果:
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(1)利用散点图或相关系数r的大小判断变量y对x是否线性相关?为什么?
(2)如果y与x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?
(最后结果精确到0.001.参考数据:![]() ,
,![]()
![]() ,
,![]() )
)
回归分析有关公式:r= ,
, ,
,![]() .
.
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
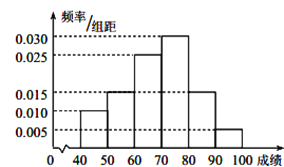
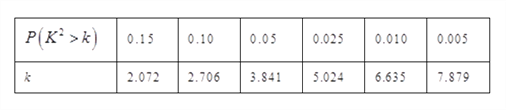
(I)在答题卡上填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
(II)将上述调査所得的频率视为概率,现从该校参与竞赛的学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:,其中
![]() .
.