题目内容
已知直线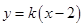
 与抛物线
与抛物线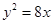 相交于
相交于 、
、 两点,
两点,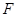 为抛物线的焦点,若
为抛物线的焦点,若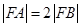 ,则
,则 的值为 。
的值为 。
解析试题分析:直线y=k(x-2)(k>0)恒过定点(2,0)即为抛物线y2=8x的焦点F,过A,B两点分别作准线的垂线,垂足分别为C,D,再过B作AC的垂线,垂足为E,设|BF|=m,因为|FA|=2|FB|,所以|AF|=2m,∴AC=AF=2m,|BD|=|BF|=m,如图,在直角三角形ABE中,AE=AC-BD=2m-m=m,AB=3m,所以cos∠BAE=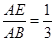 ,∴直线AB的斜率为:k=tan∠BAE=
,∴直线AB的斜率为:k=tan∠BAE=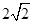 。
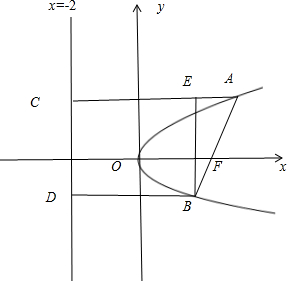
。
考点:直线与抛物线的综合应用。
点评:本题主要考查了抛物线的简单性质、共线向量及解三角形的知识,解答本题的关键是利用抛物线的定义作出直角三角形ABE,从而求得直线的斜率,体现了数形结合起来的思想。

练习册系列答案
相关题目
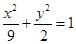 的焦点为
的焦点为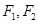 ,点
,点 在椭圆上,若
在椭圆上,若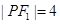 ,
,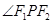 的大小为 .
的大小为 .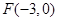 的距离比它到直线
的距离比它到直线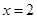 的距离大1,则点P满足的方程为 .
的距离大1,则点P满足的方程为 .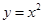 的焦点坐标是
的焦点坐标是 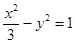 的两条渐近线的夹角大小等于 .
的两条渐近线的夹角大小等于 . 的两焦点是
的两焦点是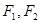 ,则其焦距长为 ,若点
,则其焦距长为 ,若点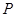 是椭圆上一点,且
是椭圆上一点,且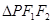 是直角三角形,则
是直角三角形,则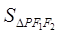 的大小是 .
的大小是 .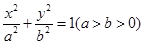 ,
,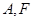 是其左顶点和左焦点,
是其左顶点和左焦点, 是圆
是圆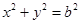 上的动点,若
上的动点,若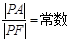 ,则此椭圆的离心率是
,则此椭圆的离心率是 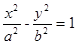 (a>0,b>0)上,C的焦距为4,则它的离心率为_____________.
(a>0,b>0)上,C的焦距为4,则它的离心率为_____________.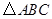 中,
中, .若以
.若以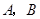 为焦点的椭圆经过点
为焦点的椭圆经过点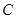 ,则该椭圆的离心率
,则该椭圆的离心率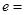 .
.