��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ��0��4������B������Ϊ��4��0������C������Ϊ��-4��0������P������AB���˶�������CP��y�ύ�ڵ�D������BD����P��D��B��������Q��y�����һ������ΪE���ӳ�DQ����Q�ڵ�F������EF��BF��
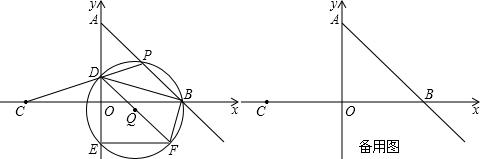
��1����ֱ��AB�ĺ�������ʽ��
��2������P���߶�AB��������A��B���㣩��ʱ��
����֤����BDE=��ADP��
����DE=x��DF=y�������y����x�ĺ�������ʽ��
��3������̽������P���˶������У��Ƿ������B��D��FΪ�����ֱ�������Σ���������ֱ�DZ�֮��Ϊ2��1��������ڣ������ʱ��P�����꣺��������ڣ���˵�����ɣ�

��1����ֱ��AB�ĺ�������ʽ��
��2������P���߶�AB��������A��B���㣩��ʱ��
����֤����BDE=��ADP��
����DE=x��DF=y�������y����x�ĺ�������ʽ��
��3������̽������P���˶������У��Ƿ������B��D��FΪ�����ֱ�������Σ���������ֱ�DZ�֮��Ϊ2��1��������ڣ������ʱ��P�����꣺��������ڣ���˵�����ɣ�
���㣺���������ε�����,��������ʽ����⼰���÷���
ר�⣺������,�ۺ���
��������1����ֱ��AB�ĺ�������ʽΪy=kx+4���ѣ�4��0�����뼴�ɣ�
��2������֤����BDO�ա�COD���ó���BDO=��CDO���ٸ��ݡ�CDO=��ADP�����ɵó���BDE=��ADP��
��������PE�����ݡ�ADP=��DEP+��DPE����BDE=��ABD+��OAB����ADP=��BDE����DEP=��ABD���ó���DPE=��OAB����֤����DFE=��DPE=45�㣬�����ݡ�DEF=90�㣬�ó���DEF�ǵ���ֱ�������Σ��Ӷ����DF=
DE����y=
x��
��3����
=2ʱ������F��FH��OB�ڵ�H�����DBO=��BFH����֤����BOD�ס�FHB��
=
=
=2���ó�FH=2��OD=2BH���ٸ��ݡ�FHO=��EOH=��OEF=90�㣬�ó��ı���OEFH�Ǿ��Σ�OE=FH=2��EF=OH=4-
OD������DE=EF�����OD�ij����Ӷ��ó�ֱ��CD�Ľ���ʽΪy=
x+
��������ֱ�߷��̼��������P�����ꣻ
��
=
ʱ������EB����֤����DEF�ǵ���ֱ�������Σ�����F��FG��OB�ڵ�G��ͬ���ɵá�BOD�ס�FGB��
=
=
=
���ó�FG=8��OD=
BG����֤���ı���OEFG�Ǿ��Σ����OD��ֵ�������ֱ��CD�Ľ���ʽ���������ֱ�߷��̼��������P�����꣮
��2������֤����BDO�ա�COD���ó���BDO=��CDO���ٸ��ݡ�CDO=��ADP�����ɵó���BDE=��ADP��
��������PE�����ݡ�ADP=��DEP+��DPE����BDE=��ABD+��OAB����ADP=��BDE����DEP=��ABD���ó���DPE=��OAB����֤����DFE=��DPE=45�㣬�����ݡ�DEF=90�㣬�ó���DEF�ǵ���ֱ�������Σ��Ӷ����DF=
| 2 |
| 2 |
��3����
| BD |
| BF |
| OB |
| HF |
| OD |
| HB |
| BD |
| FB |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
��
| BD |
| BF |
| 1 |
| 2 |
| OB |
| HF |
| OD |
| HB |
| BD |
| FB |
| 1 |
| 2 |
| 1 |
| 2 |
����⣺��1����ֱ��AB�ĺ�������ʽΪy=kx+4��
���루4��0���ã�4k+4=0�����k=-1��
��ֱ��AB�ĺ�������ʽΪy=-x+4��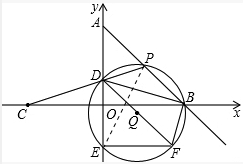
��2��������֪�ã�OB=OC����BOD=��COD=90�㣬
�֡�OD=OD�����BDO�ա�CDO���ɵá�BDO=��CDO��
�ߡ�CDO=��ADP�����BDE=��ADP��
������PE��
�ߡ�ADP�ǡ�DPE��һ����ǣ����ADP=��DEP+��DPE��
�ߡ�BDE�ǡ�ABD��һ����ǣ����BDE=��ABD+��OAB��
�ߡ�ADP=��BDE����DEP=��ABD�����DPE=��OAB��
��OA=OB=4����AOB=90�㣬���OAB=45�㣬�ɵá�DPE=45�㣬
���DFE=��DPE=45�㣬
��DF�ǡ�Q��ֱ�������DEF=90�㣬�ɵá�DEF�ǵ���ֱ�������Σ�
��DF=
DE����y=
x��
��3����BD��BF=2��1ʱ������F��FH��OB�ڵ�H��
�ߡ�DBO+��OBF=90�㣬��OBF+��BFH=90�㣬���DBO=��BFH��
�֡ߡ�DOB=��BHF=90�㣬���BOD�ס�FHB���ɵ�
=
=
=2����FH=2��OD=2BH��
�ߡ�FHO=��EOH=��OEF=90�㣬���ı���OEFH�Ǿ��Σ��ɵ�OE=FH=2��EF=OH=4-
OD��
��DE=EF����2+OD=4-
OD�����OD=
��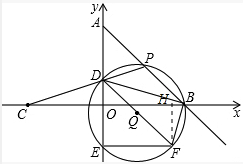 ���D��������0��
���D��������0��
����
��ֱ��CD�Ľ���ʽΪy=
x+
��
��
�ã�
��
���P��������2��2����
��
=
ʱ������EB��ͬ��2���ٿɵã���ADB=��EDP��
����ADB=��DEB+��DBE����EDP=��DAP+��DPA��
�ߡ�DEB=��DPA�����DBE=��DAP=45�㣬
���DEF�ǵ���ֱ�������Σ�
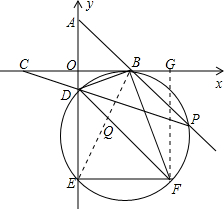 ����F��FG��OB�ڵ�G��
����F��FG��OB�ڵ�G��
ͬ���ɵá�BOD�ס�FGB����
=
=
=
��FG=8��OD=
BG��
�ߡ�FGO=��GOE=��OEF=90�㣬���ı���OEFG�Ǿ��Σ���OE=FG=8��
��EF=OG=4+2OD��
��DE=EF����8-OD=4+2OD��OD=
����õ�D������Ϊ��0��-
����
ֱ��CD�Ľ���ʽΪ��y=-
x-
��
��
�ã�
�����P��������8��-4����
������������P��������2��2����8��-4����
���루4��0���ã�4k+4=0�����k=-1��
��ֱ��AB�ĺ�������ʽΪy=-x+4��

��2��������֪�ã�OB=OC����BOD=��COD=90�㣬
�֡�OD=OD�����BDO�ա�CDO���ɵá�BDO=��CDO��
�ߡ�CDO=��ADP�����BDE=��ADP��
������PE��
�ߡ�ADP�ǡ�DPE��һ����ǣ����ADP=��DEP+��DPE��
�ߡ�BDE�ǡ�ABD��һ����ǣ����BDE=��ABD+��OAB��
�ߡ�ADP=��BDE����DEP=��ABD�����DPE=��OAB��
��OA=OB=4����AOB=90�㣬���OAB=45�㣬�ɵá�DPE=45�㣬
���DFE=��DPE=45�㣬
��DF�ǡ�Q��ֱ�������DEF=90�㣬�ɵá�DEF�ǵ���ֱ�������Σ�
��DF=
| 2 |
| 2 |
��3����BD��BF=2��1ʱ������F��FH��OB�ڵ�H��
�ߡ�DBO+��OBF=90�㣬��OBF+��BFH=90�㣬���DBO=��BFH��
�֡ߡ�DOB=��BHF=90�㣬���BOD�ס�FHB���ɵ�
| OB |
| HF |
| OD |
| HB |
| BD |
| FB |
�ߡ�FHO=��EOH=��OEF=90�㣬���ı���OEFH�Ǿ��Σ��ɵ�OE=FH=2��EF=OH=4-
| 1 |
| 2 |
��DE=EF����2+OD=4-
| 1 |
| 2 |
| 4 |
| 3 |
 ���D��������0��
���D��������0��| 4 |
| 3 |
��ֱ��CD�Ľ���ʽΪy=
| 1 |
| 3 |
| 4 |
| 3 |
��
|
|
���P��������2��2����
��
| BD |
| BF |
| 1 |
| 2 |
����ADB=��DEB+��DBE����EDP=��DAP+��DPA��
�ߡ�DEB=��DPA�����DBE=��DAP=45�㣬
���DEF�ǵ���ֱ�������Σ�
 ����F��FG��OB�ڵ�G��
����F��FG��OB�ڵ�G��ͬ���ɵá�BOD�ס�FGB����
| OB |
| GF |
| OD |
| GB |
| BD |
| FB |
| 1 |
| 2 |
| 1 |
| 2 |
�ߡ�FGO=��GOE=��OEF=90�㣬���ı���OEFG�Ǿ��Σ���OE=FG=8��
��EF=OG=4+2OD��
��DE=EF����8-OD=4+2OD��OD=
| 4 |
| 3 |
| 4 |
| 3 |
ֱ��CD�Ľ���ʽΪ��y=-
| 1 |
| 3 |
| 4 |
| 3 |
��
|
|
������������P��������2��2����8��-4����
���������⿼����һ�κ������ۺϣ��õ���֪ʶ����һ�κ��������ε����ʡ�Բ�����ʣ��ؼ����ۺ������й�֪ʶ���������ߣ��г������飮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
����ʽ��2+x2����1-x��6��չ��ʽ��x2��ϵ��Ϊ��������
| A��28 | B��31 | C��35 | D��38 |
��ͼ���ı���ABCD�ڽ���ԲO����BOD=110�㣬��BCD���ڣ�������


| A��100�� | B��110�� | C��125�� | D��135�� |

 ��ͼ��AO��ƽ�����OΪ���㣬B�ʦ���BC��BO��BC��ƽ������ɵĽ�Ϊ30�㣬AO=BO=BC=1����AC�ij�����
��ͼ��AO��ƽ�����OΪ���㣬B�ʦ���BC��BO��BC��ƽ������ɵĽ�Ϊ30�㣬AO=BO=BC=1����AC�ij�����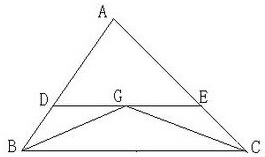
 ��ͼ��AE��ԲO�����ߣ�A���е㣬AD��OE��ֱ��������D������EC��ԲD��B��C���ҡ�BDC=62�㣬��DBE=108�㣬���OEC=
��ͼ��AE��ԲO�����ߣ�A���е㣬AD��OE��ֱ��������D������EC��ԲD��B��C���ҡ�BDC=62�㣬��DBE=108�㣬���OEC=