题目内容
 如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D.割线EC交圆D于B,C,且∠BDC=62°,∠DBE=108°,则∠OEC=
如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D.割线EC交圆D于B,C,且∠BDC=62°,∠DBE=108°,则∠OEC=考点:弦切角
专题:几何证明
分析:连接OA,OB,由已知条件得,△ADE∽△OAE,△BED∽△OEC,从而得O,C,B,D四点共圆,由此能求出结果.
解答:解:连接OA,OB,∵AE是⊙O切线∴∠OAE=90°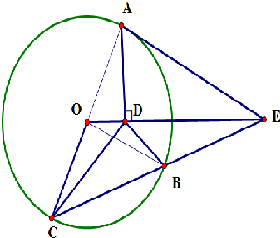
∵AD⊥OE,∴∠ADE=90°=∠OAE,又∵∠AED=∠OEA,
∴△ADE∽△OAE,∴
=
,
∴AE2=DE×OE,∵AE2=BE×CE,∴DE×OE=BE×CE,
∴
=
,
又∵∠BED=∠OEC,∴△BED∽△OEC,
∴∠BDE=∠OCE,∴O,C,B,D四点共圆,
∵OB=OC,∴∠OBC=∠OCE,∴∠ODC=∠OBC,
∴∠ODC=∠BDE,∵∠BDC=62°
∴BDE=(180°-∠BDC)÷2=59°,
∴∠OEC=180°-∠DBE-∠BDE=13°.
故答案为:13.

∵AD⊥OE,∴∠ADE=90°=∠OAE,又∵∠AED=∠OEA,
∴△ADE∽△OAE,∴
| DE |
| AE |
| AE |
| OE |
∴AE2=DE×OE,∵AE2=BE×CE,∴DE×OE=BE×CE,
∴
| DE |
| BE |
| CE |
| OE |
又∵∠BED=∠OEC,∴△BED∽△OEC,
∴∠BDE=∠OCE,∴O,C,B,D四点共圆,
∵OB=OC,∴∠OBC=∠OCE,∴∠ODC=∠OBC,
∴∠ODC=∠BDE,∵∠BDC=62°
∴BDE=(180°-∠BDC)÷2=59°,
∴∠OEC=180°-∠DBE-∠BDE=13°.
故答案为:13.
点评:本题考查角的求法,是中档题,解题时要认真审题,注意三角形相似、四点共圆等知识点的合理运用.

练习册系列答案
相关题目
在二项式(
+
)n的展开式中只有第五项的二项式系数最大,把展开式中所有的项重新排成一列,则有理项都互不相邻的概率为( )
| x |
| 2 | |||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
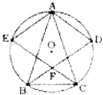 如图,AB=AC,∠ABC,∠ACB的平分线BD,CE分别交△ABC的外接圆D,E,且BD、CE相交于点F,则四边形AEFD是( )
如图,AB=AC,∠ABC,∠ACB的平分线BD,CE分别交△ABC的外接圆D,E,且BD、CE相交于点F,则四边形AEFD是( )| A、圆内接四边形 | B、菱形 | C、梯形 | D、矩形 |
已知矩阵A的逆矩阵A-1=
,则矩阵A的特征值为( )
|
| A、-1 | B、4 |
| C、-1,4 | D、-1,3 |
参数方程
(t为参数)表示的曲线不在( )
|
| A、x轴的上方 |
| B、x轴的下方 |
| C、y轴的左侧 |
| D、y轴的右侧 |
 则
则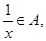 就称
就称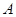 是“和谐”集合.则在集合
是“和谐”集合.则在集合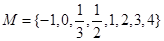 的所有非空子集中,“和谐”集合的概率是 .
的所有非空子集中,“和谐”集合的概率是 .