题目内容
将正整数1,2,3,4,…,n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算各行和各列中的任意两个数a,b(a>b)的比值
,称这些比值中的最小值为这个数表的“特征值”.若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足aij=
,当n=4时数表的“特征值”为 .
| a |
| b |
|
考点:特征值与特征向量的计算
专题:计算题,矩阵和变换
分析:写出当n=4时的图表,由特征值的定义可得答案.
解答:解:当n=4时,数表为
数表的“特征值”为
.
故答案为:
.
| 21 | 1 | 6 | 11 | 16 |
| 17 | 22 | 2 | 7 | 12 |
| 13 | 18 | 23 | 3 | 8 |
| 9 | 14 | 19 | 24 | 4 |
| 5 | 10 | 15 | 20 | 25 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查类比推理和归纳推理,属基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
i为虚数单位,(
)2=( )
| 1-i |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
已知矩阵A的逆矩阵A-1=
,则矩阵A的特征值为( )
|
| A、-1 | B、4 |
| C、-1,4 | D、-1,3 |
在极坐标系中,曲线C:p=2cosθ上任意一点P到点Q(
,
)的最大距离等于( )
| 2 |
| π |
| 4 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
参数方程
(t为参数)表示的曲线不在( )
|
| A、x轴的上方 |
| B、x轴的下方 |
| C、y轴的左侧 |
| D、y轴的右侧 |
 的定义域为A,函数
的定义域为A,函数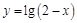 的定义域为B,则A
的定义域为B,则A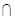 B = .
B = .