题目内容
已知椭圆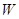 :
: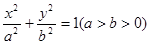 的短轴长为
的短轴长为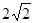 ,且斜率为
,且斜率为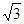 的直线
的直线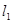 过椭圆
过椭圆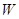 的焦点及点
的焦点及点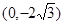 .
.
(1)求椭圆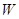 的方程;
的方程;
(2)已知直线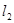 过椭圆
过椭圆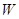 的左焦点
的左焦点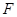 ,交椭圆于点P、Q.
,交椭圆于点P、Q.
(ⅰ)若满足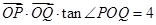 (
(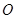 为坐标原点),求
为坐标原点),求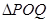 的面积;
的面积;
(ⅱ)若直线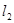 与两坐标轴都不垂直,点
与两坐标轴都不垂直,点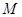 在
在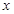 轴上,且使
轴上,且使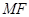 为
为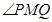 的一条角平分线,则称点
的一条角平分线,则称点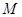 为椭圆
为椭圆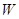 的“特征点”,求椭圆
的“特征点”,求椭圆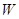 的特征点.
的特征点.
 :
: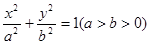 的短轴长为
的短轴长为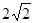 ,且斜率为
,且斜率为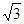 的直线
的直线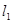 过椭圆
过椭圆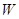 的焦点及点
的焦点及点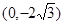 .
.(1)求椭圆
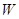 的方程;
的方程;(2)已知直线
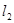 过椭圆
过椭圆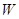 的左焦点
的左焦点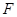 ,交椭圆于点P、Q.
,交椭圆于点P、Q.(ⅰ)若满足
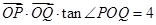 (
(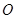 为坐标原点),求
为坐标原点),求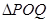 的面积;
的面积;(ⅱ)若直线
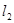 与两坐标轴都不垂直,点
与两坐标轴都不垂直,点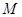 在
在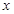 轴上,且使
轴上,且使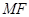 为
为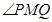 的一条角平分线,则称点
的一条角平分线,则称点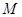 为椭圆
为椭圆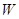 的“特征点”,求椭圆
的“特征点”,求椭圆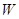 的特征点.
的特征点.(1) ;(2)(ⅰ)2,(ⅱ)
;(2)(ⅰ)2,(ⅱ)
 ;(2)(ⅰ)2,(ⅱ)
;(2)(ⅰ)2,(ⅱ)
试题分析:(1)由短轴长
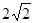 得
得 ,由焦点和点
,由焦点和点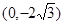 可算出斜率为
可算出斜率为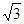 ,可以得到焦点坐标,所以可以得椭圆的方程。(2)(ⅰ)由向量的数量积公式及三角形面积公式可得出结果。(ⅱ)设直线
,可以得到焦点坐标,所以可以得椭圆的方程。(2)(ⅰ)由向量的数量积公式及三角形面积公式可得出结果。(ⅱ)设直线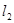 的方程,但是不需要求
的方程,但是不需要求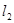 的方程,通过与椭圆联立方程组进行求解。
的方程,通过与椭圆联立方程组进行求解。试题解析:(1)由题意可知,直线
 的方程为
的方程为 , 1分
, 1分∵直线
 过椭圆
过椭圆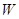 的焦点,∴该焦点坐标为
的焦点,∴该焦点坐标为 ∴
∴ 2分
2分又椭圆
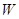 的短轴长为
的短轴长为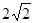 ,∴
,∴ ,∴
,∴ 3分
3分∴椭圆
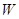 的方程为
的方程为 4分
4分(2)(ⅰ)∵
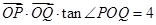
∴
 6分
6分∴
 8分
8分(ⅱ)设特征点
 ,左焦点为
,左焦点为 ,可设直线PQ的方程为
,可设直线PQ的方程为 ,
,由
 消去
消去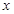 得
得
设
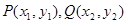 ,则
,则 10分
10分∵
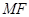 为
为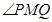 的一条角平分线,
的一条角平分线,∴
 ,即
,即 12分
12分又
 ,
,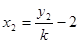 ,代入上式可得
,代入上式可得
∴
 ,解得
,解得
∴椭圆C的特征点为
 . 14分
. 14分
练习册系列答案
相关题目
 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).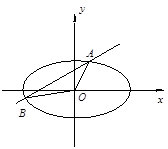
 ,
, 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过 ,
, 两点,若
两点,若 ,
, ,则椭圆的离心率为( )
,则椭圆的离心率为( )
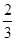


 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 的形状是( )
的形状是( )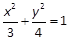 的左右两个顶点, P是该椭圆上异于A,B的任一点,则
的左右两个顶点, P是该椭圆上异于A,B的任一点,则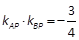 .
.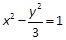 的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则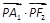 的最小值为-2.
的最小值为-2.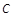 :
: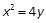 的焦点为
的焦点为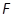 ,抛物线上一点
,抛物线上一点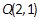 和抛物线内一点
和抛物线内一点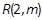
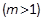 ,过点Q作抛物线的切线
,过点Q作抛物线的切线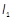 ,直线
,直线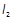 过点
过点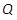 且与
且与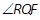 ;
;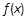 是定义在R上的奇函数,
是定义在R上的奇函数,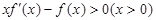 , 则不等式
, 则不等式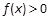 的解集是
的解集是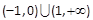 .
. +
+ =1的离心率,且e∈(
=1的离心率,且e∈( ,1),则实数k的取值范围是( )
,1),则实数k的取值范围是( ) )
) ,直线
,直线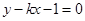 与椭圆
与椭圆 恒有公共点,则实数
恒有公共点,则实数 的取值范围是( )
的取值范围是( )