题目内容
在平面直角坐标系xOy中,直线l的参数方程为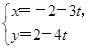 (t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为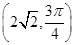 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
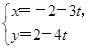 (t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.(1)求|AB|的长;
(2)以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为
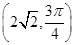 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.(1)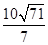 (2)
(2)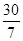
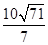 (2)
(2)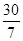
(1)把直线的参数方程代入曲线方程并化简得7t2-12t-5=0.
设A,B对应的参数分别为t1,t2,则t1+t2=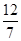 ,t1t2=-
,t1t2=-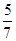 .
.
所以|AB|=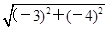 |t1-t2|?=5
|t1-t2|?=5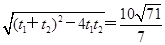
(2)易得点P在平面直角坐标系下的坐标为(-2,2),根据中点坐标的性质可得AB中点M对应的参数为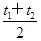 =
=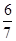 .
.
由t的几何意义可得点P到M的距离为|PM|=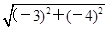 ·
·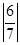 =
=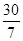 .
.
设A,B对应的参数分别为t1,t2,则t1+t2=
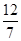 ,t1t2=-
,t1t2=-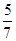 .
.所以|AB|=
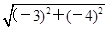 |t1-t2|?=5
|t1-t2|?=5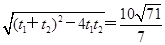
(2)易得点P在平面直角坐标系下的坐标为(-2,2),根据中点坐标的性质可得AB中点M对应的参数为
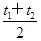 =
=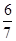 .
.由t的几何意义可得点P到M的距离为|PM|=
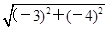 ·
·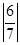 =
=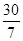 .
.
练习册系列答案
相关题目
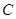 上的动点
上的动点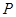 是坐标为
是坐标为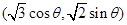 .
.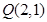 作曲线
作曲线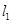 、
、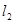 ,证明
,证明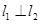 .
.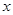 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线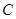 的极坐标方程为
的极坐标方程为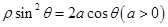 ,过点
,过点 的直线
的直线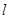 的参数方程为
的参数方程为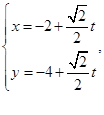 (
(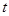 为参数),直线
为参数),直线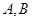 两点.
两点.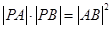 ,求
,求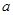 的值.
的值.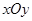 中,
中,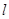 是过定点
是过定点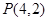 且倾斜角为
且倾斜角为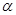 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点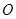 为极点,以
为极点,以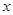 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线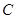 的极坐标方程为
的极坐标方程为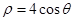 .
.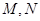 ,求
,求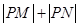 的取值范围.
的取值范围.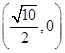 作倾斜角为α的直线与曲线x2+2y2=1交于点M、N,求|PM|·|PN|的最小值及相应的α的值.
作倾斜角为α的直线与曲线x2+2y2=1交于点M、N,求|PM|·|PN|的最小值及相应的α的值.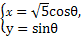 (0≤θ<π)和
(0≤θ<π)和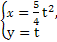 (t∈R),求它们的交点坐标.
(t∈R),求它们的交点坐标.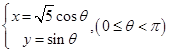 和
和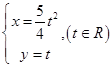 ,它们的交点坐标为____________
,它们的交点坐标为____________ 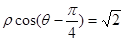 与圆
与圆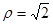 的公共点个数是________.
的公共点个数是________.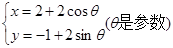 .
.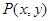 ,求
,求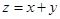 的最大值.
的最大值.