题目内容
9.有下列命题(1)函数f(x)=4sin(2x+$\frac{π}{3}$)(x∈R)的表达式可改写为y=4cos(2x-$\frac{π}{6}$);
(2)函数y=cos(sinx)(x∈R)为偶函数;
(3)函数y=sin|x|是周期函数,且周期为2π;
(4)若cosα=cosβ,则α-β=2kπ,k∈Z;
(5)设函数f(x)=$\frac{(x+1)^{2}+sinx}{{x}^{2}+1}$的最大值为M,最小值为m,则M+m=4,其中正确的命题序号是(1)(2).
分析 根据诱导公式,可判断(1);根据偶函数的定义,可判断(2);根据周期函数的定义,可判断(3);根据诱导公式,及余弦的定义,可判断(4);根据函数奇偶性的性质,可判断(5);
解答 解:f(x)=4sin(2x+$\frac{π}{3}$)=4cos[$\frac{π}{2}$-(2x+$\frac{π}{3}$)]=4cos(-2x+$\frac{π}{6}$)=4cos(2x-$\frac{π}{6}$),故(1)正确;
令f(x)=y=cos(sinx),则f(x)=cos[sin(-x)]=cos(-sinx)=cos(sinx),故函数为偶函数,故(2)正确,
函数y=sin|x|不是周期函数,故(3)错误;
若cosα=cosβ,则α-β=2kπ,k∈Z,或α+β=2kπ,k∈Z,故(4)错误;
函数f(x)=$\frac{(x+1)^{2}+sinx}{{x}^{2}+1}$=1+$\frac{2x+sinx}{{x}^{2}+1}$,其中y=$\frac{2x+sinx}{{x}^{2}+1}$为奇函数,
设y=$\frac{2x+sinx}{{x}^{2}+1}$的最大值为N,最小值为n,则N+n=0,M=N+1,m=n+1,
∴M+m=2,故(5)错误.
故答案为:(1)(2)
点评 本题以命题的真假判断为载体,考查了函数的奇偶性,周期性,诱导公式等知识点,难度中档.

练习册系列答案
相关题目
19.不等式|x+1|-|x-3|≥0的解集是( )
| A. | [1,+∞) | B. | (-∞,-1]∪[1,+∞) | C. | [-1,3] | D. | (-∞,1] |
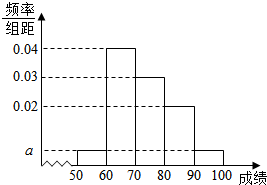 某校1000名学生期中考试数学成绩的频率分布直方图如右图所示,其中成绩分组区间是:[50,60),[60,70),[70,
某校1000名学生期中考试数学成绩的频率分布直方图如右图所示,其中成绩分组区间是:[50,60),[60,70),[70,
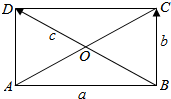 如图所示,已知在矩形ABCD中,|$\overrightarrow{AD}$|=4$\sqrt{3}$,|$\overrightarrow{AB}$|=8,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{BD}$=$\overrightarrow{c}$,求|$\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}$|
如图所示,已知在矩形ABCD中,|$\overrightarrow{AD}$|=4$\sqrt{3}$,|$\overrightarrow{AB}$|=8,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{BD}$=$\overrightarrow{c}$,求|$\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}$|