题目内容
14.在正项数列{an}中,a1=$\frac{1}{3}$,an+1=an+($\frac{{a}_{n}}{n}$)2(n∈N*)(1)判断数列{an}的单调性,并证明你的结论;
(2)求证:对n∈N*都有:$\frac{1}{3}$≤an<1.
分析 (1)数列{an}为单调递增数列,作差证明即可;
(2)易知$\frac{1}{3}$≤an,再利用放缩法证明an<1即可.
解答 解:(1)数列{an}为单调递增数列,证明如下,
∵an+1=an+($\frac{{a}_{n}}{n}$)2,
∴an+1-an=($\frac{{a}_{n}}{n}$)2>0,
∴数列{an}为单调递增数列;
(2)证明:∵数列{an}为单调递增数列,
又∵a1=$\frac{1}{3}$,
∴$\frac{1}{3}$≤an,
①a1=$\frac{1}{3}$<1,
②a2=$\frac{1}{3}$+$\frac{1}{9}$=$\frac{4}{9}$<1,
③a3=$\frac{4}{9}$+$\frac{4}{81}$=$\frac{40}{81}$<1,
④假设an<1,
则an+1=a1+$\frac{{(a}_{1})^{2}}{{1}^{2}}$+$\frac{({a}_{2})^{2}}{{2}^{2}}$+…+$\frac{({a}_{n-1})^{2}}{(n-1)^{2}}$+$\frac{{{a}_{n}}^{2}}{{n}^{2}}$
=a1+$\frac{1}{9}$+$\frac{4}{81}$+…+$\frac{({a}_{n-1})^{2}}{(n-1)^{2}}$+$\frac{{{a}_{n}}^{2}}{{n}^{2}}$
<$\frac{1}{3}$+$\frac{1}{9}$+$\frac{4}{81}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{(n-1)^{2}}$+$\frac{1}{{n}^{2}}$
<$\frac{40}{81}$+$\frac{1}{2•3}$+…+$\frac{1}{(n-2)(n-1)}$+$\frac{1}{n(n-1)}$
<$\frac{40}{81}$+$\frac{1}{2}$-$\frac{1}{n}$<1;
故$\frac{1}{3}$≤an<1.
点评 本题考查了数列的单调性的判断与证明,同时考查了放缩法与裂项求和法的应用.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案| A. | (0,$\frac{1+ln3}{3}$) | B. | ($\frac{1}{2}$,$\frac{1+ln3}{3}$] | C. | ($\frac{1+ln3}{3}$,1) | D. | [$\frac{1+ln3}{3}$,1) |
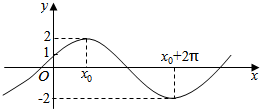 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).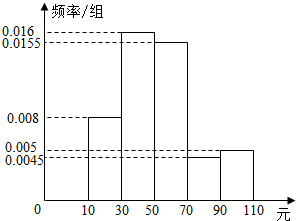 一家电信公司在某大学对学生每月的手机话费进行抽样调查,随机抽取了100名学生,将他们的手机话费情况进行统计分析,绘制成频率分布直方图(如图所示).如果该校有大学生10000人,请估计该校每月手机话费在[50,70)的学生人数是3100.
一家电信公司在某大学对学生每月的手机话费进行抽样调查,随机抽取了100名学生,将他们的手机话费情况进行统计分析,绘制成频率分布直方图(如图所示).如果该校有大学生10000人,请估计该校每月手机话费在[50,70)的学生人数是3100.