题目内容
11.已知指数函数y=ax(a>0,且a≠1)的图象经过点(1,3).(1)求函数的解析式;
(2)求当x=-1,0,2时的函数值;
(3)画出函数的图象;
(4)叙述函数的性质.
分析 (1)通过待定系数法求出a的值即可;(2)分别将x=-1,0,2代入函数的解析式求出函数值即可;(3)画出函数图象即可;(4)根据图象读出函数的性质即可.
解答 解:(1)将(1,3)代入y=ax,
得:a=3,∴y=3x;
(2)x=-1时:y=$\frac{1}{3}$,
x=0时:y=1,
x=2时:y=9;
(3)画出函数图象,如图示: ,
,
(4)函数的定义域是R,值域是(0,+∞),
函数在R上单调递增,恒过(0,1)点.
点评 本题考查了指数函数的图象和性质,考查求函数的解析式问题,是一道基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
16.已知O为坐标原点,实数x,y满足$\left\{\begin{array}{l}{x-y+1≤0}\\{3x+4y≤12}\\{x-1≥0}\end{array}\right.$,P(x,y)为该不等式组所表示的平面区域内任意一点,使z=x+2y取最大值的点为A点,则|OP|•|AO|•cos∠AOP的最大值等于( )
| A. | $\frac{97}{16}$ | B. | $\frac{11}{2}$ | C. | $\frac{167}{28}$ | D. | $\frac{38}{7}$ |
4.如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=( )
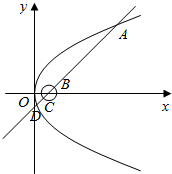

| A. | 13 | B. | 14 | C. | 15 | D. | 16 |