Question

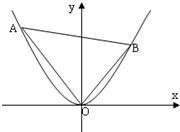在平面直角坐标系xOy中，抛物线y=x²上异于坐标原点O的两不同动点A、B满足AO⊥BO（如图所示）．则△AOB得重心G（即三角形三条中线的交点）的轨迹方程为 ________；

Answer 1

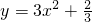
分析：设出AB的方程，A，B的坐标，进而把直线与抛物线方程联立消去y，根据韦达定理求得x₁+x₂和x₁x₂的表达式，进而利用抛物线方程求得y₁y₂=的表达式，进而根据AO⊥BO推断出x₁x₂+y₁y₂=0，求得b，设△AOB的重心为G（x，y），则x和y的表达式可得，联立后消去k则x和y的关系式可得．
解答：显然直线AB的斜率存在，记为k，AB的方程记为：y=kx+b，（b≠0），A（x₁，y₁），B（x₂，y₂），将直线方程代入y=x²得：x²-kx-b=0，则有：
△=k²+4b＞0①，x₁+x₂=k②，x₁x₂=-b③，又y₁=x₁²，y₂=x₂²
∴y₁y₂=b²；
∵AO⊥BO，∴x₁x₂+y₁y₂=0，
得：-b+b²=0且b≠0，
∴b=1，代入①验证，满足；
故y₁+y₂=k（x₁+x₂）+2=k²+2；
设△AOB的重心为G（x，y），
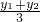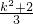则x==④，y==⑤，
由④⑤两式消去参数k得：G的轨迹方程为．
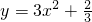故答案为：．
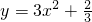点评：本题主要考查了抛物线的简单性质．上述求轨迹的方法称为“参数法”，一般先设法将动点坐标用“参数”表示，再消参数．