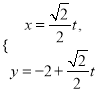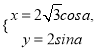题目内容
【题目】已知动点![]() 是圆
是圆![]() :
: ![]() 上的任意一点,点
上的任意一点,点![]() 与点
与点![]() 的连线段的垂直平分线和
的连线段的垂直平分线和![]() 相交于点
相交于点![]() .
.
(I)求点![]() 的轨迹
的轨迹![]() 方程;
方程;
(II)过坐标原点![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于点
于点![]() ,
, ![]() 两点,直线
两点,直线![]() 与坐标轴不重合.
与坐标轴不重合. ![]() 是轨迹
是轨迹![]() 上的一点,若
上的一点,若![]() 的面积是4,试问直线
的面积是4,试问直线![]() ,
, ![]() 的斜率之积是否为定值,若是,求出此定值,否则,说明理由.
的斜率之积是否为定值,若是,求出此定值,否则,说明理由.
【答案】(1) ![]() (2) 直线
(2) 直线![]() ,
, ![]() 的斜率之积是定值
的斜率之积是定值![]()
【解析】试题分析:(I)由题意得![]() ,利用椭圆的定义,得点
,利用椭圆的定义,得点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆,进而得到椭圆的方程;
为焦点的椭圆,进而得到椭圆的方程;
(II)设直线![]() 的方程为
的方程为![]() ,联立发出来,求解
,联立发出来,求解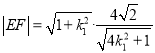 ,设
,设![]() 所在直线方程为
所在直线方程为![]() ,联立椭圆方程得
,联立椭圆方程得![]() 的坐标,再求得点
的坐标,再求得点![]() 到直线
到直线![]() 的距离,根据面积列出方程,得到
的距离,根据面积列出方程,得到![]() 的方程,即可求解
的方程,即可求解![]() 的值.
的值.
试题解析:
(I)由题意, ![]() ,又∵
,又∵![]()
∴![]() ,
,
∴点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆,其中
为焦点的椭圆,其中![]() ,
, ![]()
∴椭圆![]() 的方程为
的方程为![]() .
.
(II)设直线![]() 的方程为
的方程为![]() ,联立
,联立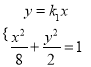 ,得
,得![]()
∴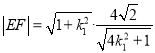
设![]() 所在直线方程为
所在直线方程为![]() ,联立椭圆方程得
,联立椭圆方程得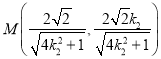 或
或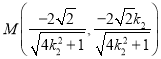 ,
,
点![]() 到直线
到直线![]() 的距离
的距离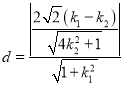 .
.
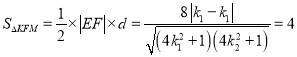
∴![]() ,
,
即![]() ,解得
,解得![]() ,
,
∴直线![]() ,
, ![]() 的斜率之积是定值
的斜率之积是定值![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】借助计算器填写下表:
|
|
|
|
|
0 | ||||
1 | ||||
10 | ||||
20 | ||||
30 | ||||
50 | ||||
70 | ||||
100 | ||||
150 | ||||
200 | ||||
250 | ||||
300 |
观察表中的变化并归纳各函数递增的规律:
(1)一次函数![]() 与幂函数
与幂函数![]() 之间比较得出的规律;
之间比较得出的规律;
(2)幂函数![]() 与指数函数
与指数函数![]() 之间比较得出的规律;
之间比较得出的规律;
(3)指数函数![]() 与
与![]() 之间比较得出的规律.
之间比较得出的规律.