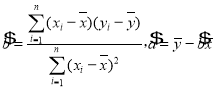题目内容
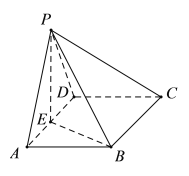
【题目】如图,已知四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() ,F,G分别是
,F,G分别是![]() 的中点.
的中点.
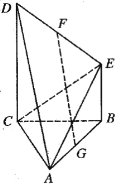
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点O,连接
的中点O,连接![]() ,根据条件可证平面
,根据条件可证平面![]() 平面
平面![]() ,从而可证明.
,从而可证明.
(Ⅱ)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由
,由![]() 得
得![]() ,故以点O为坐标原点,
,故以点O为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立如图所示的空间直角坐标系,利用向量法求二面角.
轴建立如图所示的空间直角坐标系,利用向量法求二面角.
(Ⅰ)证明:如图,取![]() 的中点O,连接
的中点O,连接![]() .
.
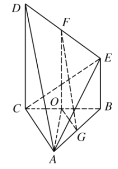
![]() 点
点![]() 分别为
分别为![]() 的中点,点O为
的中点,点O为![]() 的中点,
的中点,
![]() 为梯形
为梯形![]() 的中位线,
的中位线,![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
同理,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(Ⅱ)![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,
故以点O为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
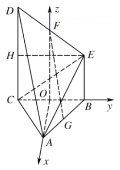
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,作
,作![]() ,垂足为点H.
,垂足为点H.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,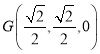 ,
,
 ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由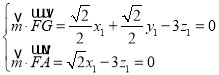
得![]() ,令
,令![]() ,
,![]() ;
;
设平面![]() 的法向量为
的法向量为![]() ,
,
由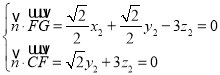
得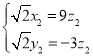
令![]() .
.
设二面角![]() 的大小为
的大小为![]() ,
,
由图可知,二面角![]() 为锐角,
为锐角,
则![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]()

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
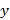
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中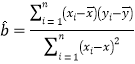
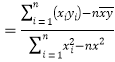 .
.
【题目】某工厂新购置甲、乙两种设备,分别生产A,B两种产品,为了解这两种产品的质量,随机抽取了200件进行质量检测,得到质量指标值的频数统计表如下:
质量指标值 |
|
|
|
|
|
| 合计 |
A产品频数 | 2 | 6 | a | 32 | 20 | 10 | 80 |
B产品频数 | 12 | 24 | b | 27 | 15 | 6 | n |
产品质量2×2列联表
产品质量高 | 产品质量一般 | 合计 | |
A产品 | |||
B产品 | |||
合计 |
附: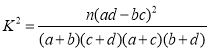
|
|
|
|
|
|
|
|
(1)求a,b,n的值,并估计A产品质量指标值的平均数;
(2)若质量指标值大于50,则说明该产品质量高,否则说明该产品质量一般.请根据频数表完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为质量高低与引入甲、乙设备有关.
的把握认为质量高低与引入甲、乙设备有关.